4 Measuring nestedness

Klementyna Gawecka
session 22/03/2023

Slides for this exercise session are available here.

4.1 Introduction

Nestedness is a measure of the structure of bipartite networks. Ecological networks, such as plant-pollinator networks, are often nested.

There there are many different measures of nestedness. We will focus on a modified version of the NODF measure (Almeida-Neto et al., 2008) which was used, for example, in Fortuna et al. (2019) to investigate networks of bacteria and phage.

The exercises in Part 1 are to be solved on paper. Please take a picture or scan your work, name the file as surname_name followed by the extension (png, jpg, pdf, etc.), and send the file to klementyna.gawecka@uzh.ch.

The exercises in Part 2 must be solved in R and submitted as an RScript.

In the section R Scripts you find code that will help you to solve the exercises in Part 2.

Almeida-Neto, M., Guimarães, P., Guimarães, P.R., Ulrich, W.: A consistent metric for nestedness analysis in ecological systems: reconciling concept and measurement. Oikos, 1227–1239 (2008). DOI 10.1111/j.2008.0030-1299.16644.xh
Fortuna, M.A., Barbour, M.A., Zaman, L., Hall, A.R., Buckling, A. and Bascompte, J.: Coevolutionary dynamics shape the structure of bacteria‐phage infection networks. Evolution 1001-1011 (2019). DOI 10.1111/evo.13731

4.2 R Scripts

The following code downloads network M_SD_024 from the Web of Life.

# Import the rjson package
library(rjson) 

# Define the url associated with the network to be downloaded
json_url <- "https://www.web-of-life.es/get_networks.php?network_name=M_SD_024"

# Download the network (as a dataframe)
network_data <- jsonlite::fromJSON(json_url)

The following code plots the network using functions from the R `igraph’ package.

# Import the igraph and dplyr packages
library(igraph)
library(dplyr)

# Select the relevant columns and create the igraph object 
network_graph <- network_data %>% 
  select(species1, species2, connection_strength) %>% 
  graph_from_data_frame(directed=FALSE)

# Convert the network into bipartite format
V(network_graph)$type <- bipartite.mapping(network_graph)$type 

# Assign different colours to plants and seed dispersers
V(network_graph)$color <- ifelse(V(network_graph)$type == TRUE, "blue", "orange")

# Plot network using bipartite layout
plot(network_graph,
     layout=layout_as_bipartite, 
     arrow.mode=0,
     vertex.label=NA,
     vertex.size=4,
     asp=0.2)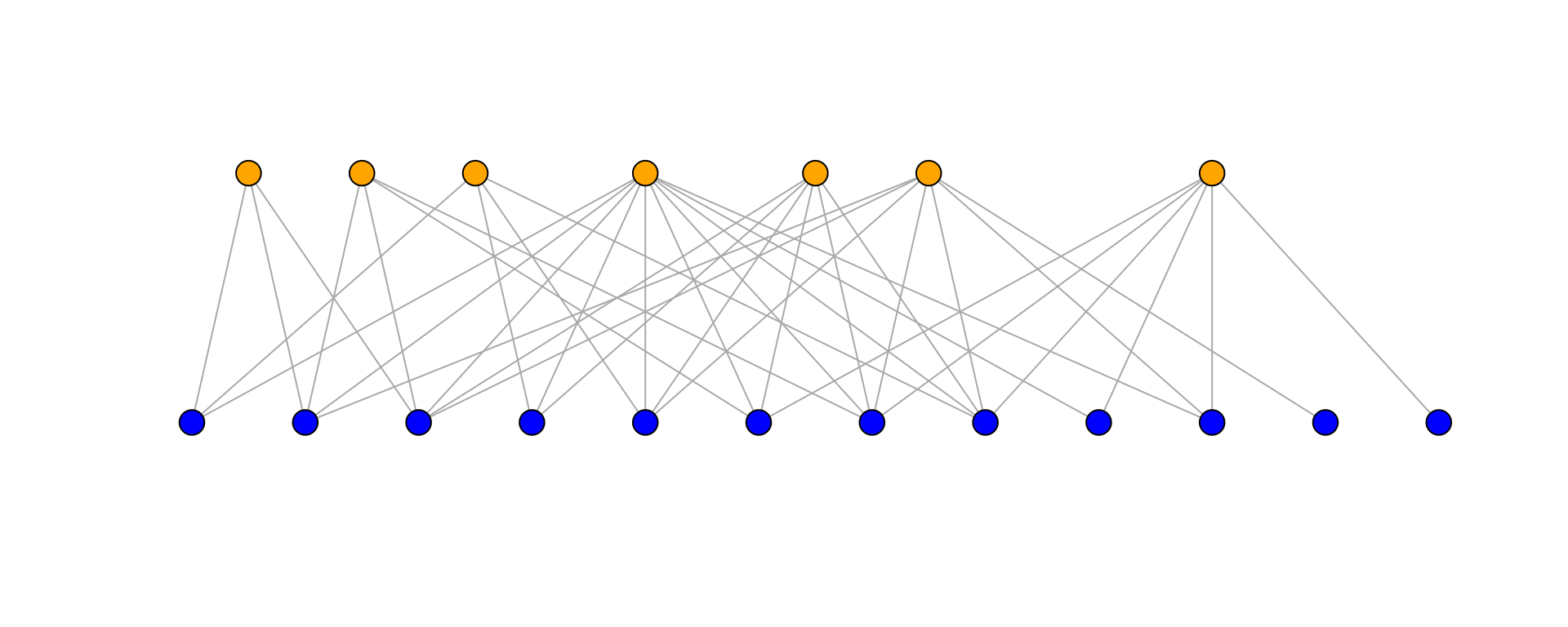

The following code computes the nestedness of the network using the nestedness function from rweboflife package.

# Import the rweboflife package
library(rweboflife)

# Convert the igraph object into incidence matrix 
network_matrix <- as_incidence_matrix(network_graph, attr="connection_strength", names=TRUE, sparse=FALSE)

# Convert elements into numeric values 
class(network_matrix) <- "numeric"

# Compute network nestedness
rweboflife::nestedness(network_matrix)

## [1] 0.6318829

The nestedness function in rweboflife package uses the Fortuna et al. (2019) nestedness measure. Below is the R code for this function as implemented in the package.

nestedness <- function(B){

  # Get number of rows and columns
  nrows <- nrow(B)
  ncols <- ncol(B)
  
  # Compute nestedness of rows
  nestedness_rows <- 0
  for(i in 1:(nrows-1)){
    for(j in (i+1): nrows){
      
      c_ij <- sum(B[i,] * B[j,])      # Number of interactions shared by i and j
      k_i <- sum(B[i,])               # Degree of node i
      k_j <- sum(B[j,])               # Degree of node j
        
      if (k_i == 0 || k_j==0) {next}  # Handle case if a node is disconnected
        
      o_ij <- c_ij / min(k_i, k_j)    # Overlap between i and j
        
      nestedness_rows <- nestedness_rows + o_ij
    }
  }
  
  # Compute nestedness of columns
  nestedness_cols <- 0
  for(i in 1: (ncols-1)){
    for(j in (i+1): ncols){
      
      c_ij <- sum(B[,i] * B[,j])      # Number of interactions shared by i and j
      k_i <- sum(B[,i])               # Degree of node i
      k_j <- sum(B[,j])               # Degree of node j
      if (k_i == 0 || k_j==0) {next}  # Handle case if a node is disconnected.

      o_ij <- c_ij / min(k_i, k_j)    # Overlap between i and j

      nestedness_cols <- nestedness_cols + o_ij         
    }
  }
  
  # Compute nestedness of the network
  nestedness <- (nestedness_rows + nestedness_cols) / ((nrows * (nrows - 1) / 2) + (ncols * (ncols - 1) / 2))
  
  return(nestedness)
}

4.3 Exercises - Part 1 (on paper)

Once you have completed the following exercises on paper, please take a picture or scan your work and name the file as: surname_name followed by the extension (png, jpg, pdf, etc.). Send the file to klementyna.gawecka@uzh.ch.

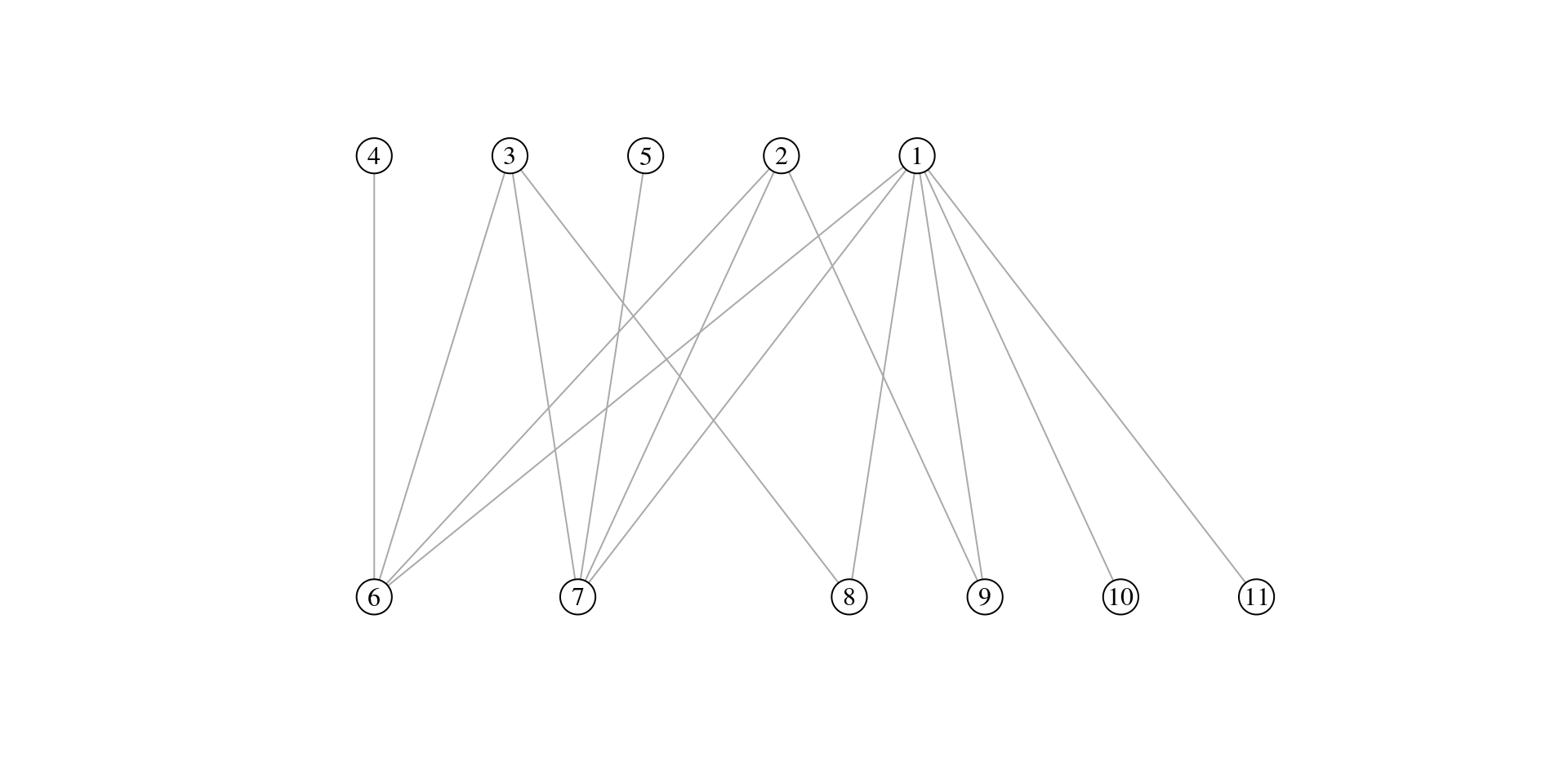
Exercise 1: For the bipartite graph drawn below:

write down the incidence matrix B
compute connectance C

Exercise 2: Compute the nestedness of the bipartite graph defined by the incidence matrix \(B_2\).

\[ \\B_2 = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \]

4.4 Exercises - Part 2 (R)

Exercise 3: Use R to check the result you obtained in Exercise 2.

Hint: Use the following code to create the incidence matrix \(B_2\). Then, calculate its nestedness using the nestedness function (see example above).

B_2 <- matrix(c(1,1,1,1,0,
                1,1,1,0,1,
                1,0,1,0,0,
                1,1,0,0,0,
                1,0,0,0,0,
                1,0,0,0,0), nrow=5, ncol=6)

Exercise 4: For the mutualistic plant-pollinator network M_PL_052:

Download the network from the Web of Life
Plot the network in R using the bipartite layout.
Compute connectance C of the network.
Compute nestedness of the network.