7 Simulating networks

Alessandro Vindigni and Fernando Pedraza
session 28/03/2023

7.1 Models for simulating networks

Theoretical models used for generating networks can be useful for at least two reasons. First, they can help us understand the underlying processes driving the structure of ecological networks. Second, if the models perform well, they can help us expand the number of networks we work with.

Several theoretical models exist for generating artificial networks. Most were originally proposed for food webs and later were adapted for mutualistic interactions. Here we will explore how two different models (the cascade and the niche models) proposed by Pires et al. 2011 perform in reproducing the structural properties of a set of mutualistic networks. Next we provide a brief description of the assumptions of each model. When describing the models, for simplicity, we will refer to one guild as the “animals” and the other as “plants”. Both models establish interactions based on the traits of species. These traits are numbers that are randomly assigned to each animal and plant species in the community.

7.1.1 The cascade model

The cascade model assumes that interactions are based on hierarchical feeding. In other words, a species can interact with species whose trait values are smaller than their own. The algorithm for the model is the following:

Assign a random trait value drawn from a uniform distribution on the interval [0,1] to each animal and plant in the community. For mutualistic networks, these trait values are drawn independently for each guild.
Compare the traits of all animals and plants to determine whether or not they interact. Animals can potentially interact with plants whose trait values are smaller than their own but can never interact with other animals.
Determine the probability of interactions occurring: \(q = E/T\), where \(E\) is the number of recorded interactions and \(T\) is the number of possible interactions after species positions are defined.

7.1.2 The niche model

The niche model also establishes interactions based on species’ traits. Yet, it assumes that animals can only interact with plants whose traits fall within a range. The algorithm for the model is the following:

Assign a random trait value drawn from a uniform distribution on the interval [0,1] to each animal and plant in the community. For mutualistic networks, these trait values are drawn independently for each guild.
For each consumer (\(i\)) calculate it’s niche range(\(r_i\)). \(r_i=xn_i\), where \(0 ≤ x ≤ 1\) is a random variable with a beta-distributed probability density function \(p(x) = \beta(1-x)(\beta-1)\) with \(\beta=(1/2C) - 1\).
Determine the range center (\(c_i\)) for each species. \(c_i\) is a uniformly random number between \(r_i/2\) and \(min(n_i, 1 - r_i/2)\).
Determine the interaction interval (\(I(D_i)\)) for each species. \(I(D_i) = [c_i - r_i/2, c_i + r_i/2]\).
Establish interactions between plants and animals. An animal \(i\) will interact with all plants \(j\) whose \(n_j\) falls within its interaction interval.

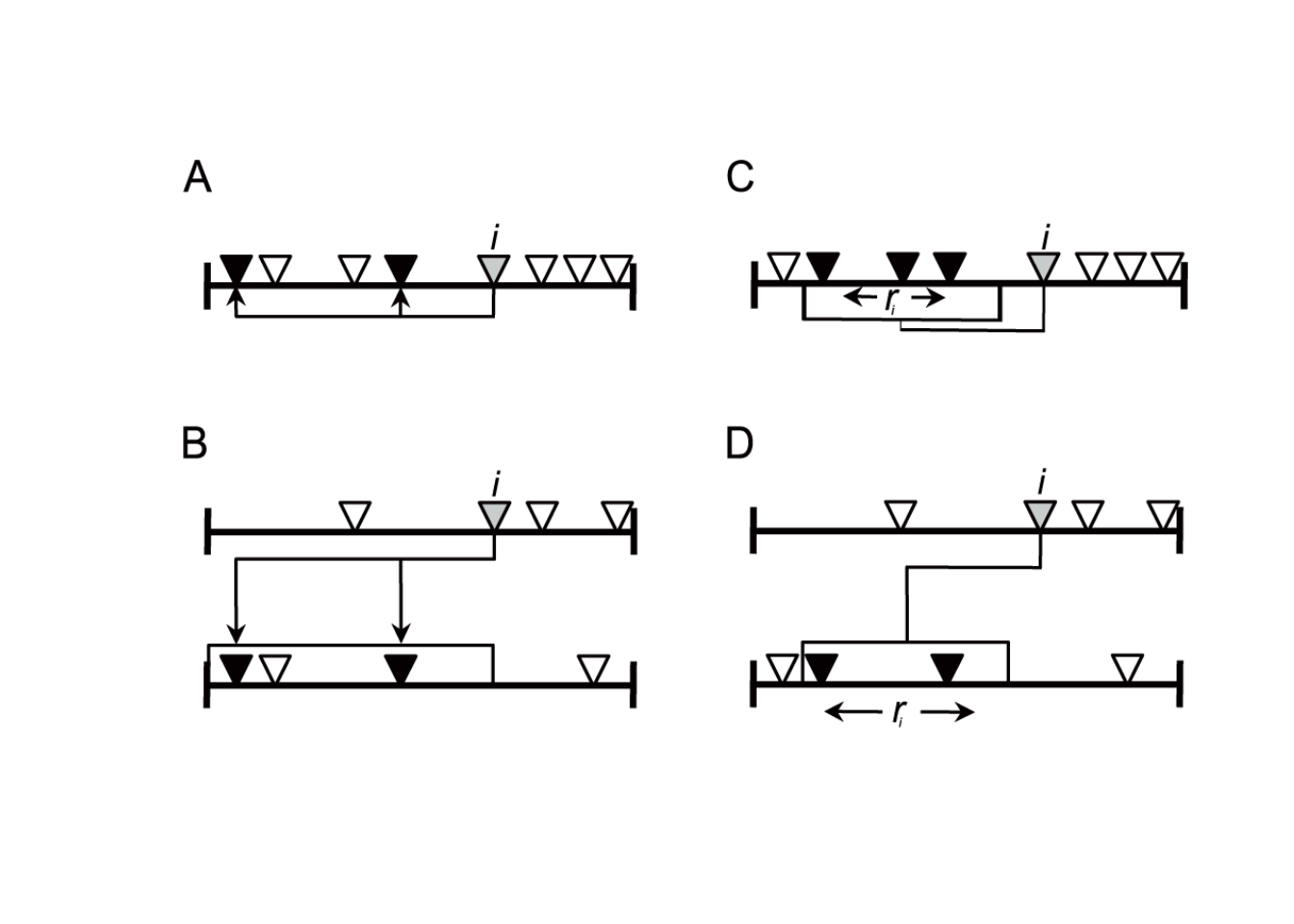
Graphical representation of the models. The cascade model is illustrated in the left column and the niche model in the right column. The top row illustrates the models for a food web. The bottom row illustrates the models for a mutualistic network. This figure is reproduced from Pires et al. 2011.

Figure 7.1: Graphical representation of the models. The cascade model is illustrated in the left column and the niche model in the right column. The top row illustrates the models for a food web. The bottom row illustrates the models for a mutualistic network. This figure is reproduced from Pires et al. 2011.

7.2 Running the models for one community

We are providing you the code to implement the models. However, because simulating a network can be a rather slow process and R is already plenty slow(!), we coded the functions in the Julia language (Julia is a relatively new language that merges readability with speed). The code is stored on the R server, in ecological_networks_2023/downloads/Functions/build_networks.jl. However, to keep things manageable, we will be running the Julia code from R. To do this, we will use the JuliaCall package.

To initialise a Julia session from R, run the following commands:

# load the package
library(JuliaCall)

# if the package is not installed, run the following command:
# install.packages(JuliaCall)

# Initialise a Julia session from R
julia_setup("/home/ubuntu/julia-1.8.1/bin/")

# Then install some required packages (note you only have to do this once!)
julia_install_package("Distributions") 
julia_install_package("Random") 

# Source the functions that we will use to run the models (change test_student with your user name)
julia_source("/home/test_student/ecological_networks_2023/downloads/Functions/build_networks.jl")

Now we can run the model to generate networks. The function to run the cascade model is build_cascade_networks while build_niche_networks runs the niche model. Both functions require three arguments:

the number of animal species in the community.
the number of plant species in the community.
the target the connectance (i.e. the connectance that the artificial network should have).

The function returns an incidence matrix that corresponds to the requested artificial network. For example, to generate an artificial incidence matrix composed of 20 animals and 30 plants with a target connectance of 0.2 using the niche model, you would run the following command:

# run the julia code with the specified parameters and store the incidence matrix. 
niche_artificial <- julia_eval("build_niche_networks(20, 30, 0.2)")

You can then analyse the artificial incidence matrix like you have done so in the past days. For example, you can plot it or calculate some structural properties (e.g. nestedness or modularity).

Exercise 1

Generate two artificial incidence matrices, one using the cascade model and the other using the niche model, for a community composed of 10 animals and 10 plants with a target connectance of 0.3. Visualise the networks and comment on any structural differences you see.

7.3 Compare artificial networks against empirical ones

Using the niche and the cascade models, we have created a set of artificial networks and stored them in a file. To load that data run the following commands:

# this block has to occur in sequence 
# clean up
rm(list=ls())
# load simulated networks
load("~/ecological_networks_2023/downloads/Data/03-28_simulating_networks/artificial_matrices.Rda")
artificial_networks <- mget(ls())

As you can check, the variable artificial_networks is a named list with elements

simulated_nw_names <- names(artificial_networks)
simulated_nw_names

##  [1] "M_PL_008_cascade_inc" "M_PL_008_niche_inc"   "M_PL_025_cascade_inc"
##  [4] "M_PL_025_niche_inc"   "M_PL_037_cascade_inc" "M_PL_037_niche_inc"  
##  [7] "M_PL_038_cascade_inc" "M_PL_038_niche_inc"   "M_PL_059_cascade_inc"
## [10] "M_PL_059_niche_inc"   "M_SD_014_cascade_inc" "M_SD_014_niche_inc"  
## [13] "M_SD_021_cascade_inc" "M_SD_021_niche_inc"   "M_SD_024_cascade_inc"
## [16] "M_SD_024_niche_inc"   "M_SD_025_cascade_inc" "M_SD_025_niche_inc"  
## [19] "M_SD_029_cascade_inc" "M_SD_029_niche_inc"

each element containing the incidence matrix of a simulated network. As you can read from the list above, the model used in the simulation is defined in the name of each element. The initial part of the name refers, instead, to the corresponding empirical network of web of life.

Before proceeding, it is useful to load the following packages:

library(igraph)
library(rweboflife)
library(formattable)

We have also pre-computed the connectance, nestedness, and modularity of the 10 considered empirical networks. You can load that data as well from file:

# load indices computed for empirical networks
load("~/ecological_networks_2023/downloads/Data/03-28_simulating_networks/empirical_nw_df.Rda")
empirical_nw_df %>% formattable()

interaction_type	network_name	nestedness	connectance	modularity
Pollination	M_PL_008	0.3978981	0.2535885	0.3428711
Pollination	M_PL_025	0.5615351	0.2500000	0.2825811
Pollination	M_PL_037	0.2866498	0.1800000	0.4926698
Pollination	M_PL_038	0.3549508	0.2351190	0.4081077
Pollination	M_PL_059	0.9346739	0.4201183	0.1748661
SeedDispersal	M_SD_014	0.8245156	0.4448529	0.1875213
SeedDispersal	M_SD_021	0.6623913	0.2559524	0.2577670
SeedDispersal	M_SD_024	0.6318829	0.4761905	0.2321875
SeedDispersal	M_SD_029	1.0000000	0.5000000	0.2650000
SeedDispersal	M_SD_025	0.5714092	0.3307692	0.2985398

Your goal is to produce a similar dataset using the simulated networks. To help you in this task, we will guide you through the computation of nestedness, modularity, and connectance for just one artificial network.

Assume you want to focus on the 4th artificial network of the list named

nw_label <- 4 # 4th simulated network
simulated_nw_names[nw_label]

## [1] "M_PL_025_niche_inc"

You can extract the incidence matrix as follows

  # extract incidence matrix form the list 
  inc_matrix <- artificial_networks[[nw_label]]

and compute the relative nestedness using the rweboflife package

  # compute netsedness 
  nest <- rweboflife::nestedness(inc_matrix)
  nest

## [1] 0.4732627

and the relative modularity (following the procedure discussed in a previous exercise session)

  # compute modularity
  nw_graph <- graph_from_incidence_matrix(inc_matrix) 
  modules <- cluster_fast_greedy(nw_graph)
  mm <- modularity(modules)
  mm

## [1] 0.3818828

If you wish to compute the connectance from the incidence matrix (instead of using the edge list as in the first exercise session), we provide you a helping function:

connectance_from_inc_matrix <- function(M){
  # Make sure we are working with a matrix
  M <- as.matrix(M)
  # Binarize the matrix
  mat <- as.matrix((M>0))
  class(mat) <- "numeric"
  
  # extract dimensions
  num_rows <- nrow(mat)
  num_cols <- ncol(mat)
  
  # obtain number of links
  links <- sum(mat)
  
  # compute connectance
  con <- links/(num_rows * num_cols)
  
  # return
  return(con)
}

Then you can apply this function directly to the incidence matrix of simulated networks:

conn <- connectance_from_inc_matrix(inc_matrix)
conn

## [1] 0.2727273

Exercise 2

Using the data and the commands provided above, produce a pair of plots (box plot, scatter plot, etc.) that highlight the differences between the observed and the predicted values of modularity and nestedness.
Comment on the differences between the values predicted using either the cascade or the niche model.