5 Null models
Jordi Bascompte & Fernando Pedraza
session 23/03/2023
5.1 Null models by hand
In this section you will perform a randomization by hand of the provided networks using the null models covered during our morning lecture. Use R to generate random numbers (using the runif() function) and for your operations.
- Consider a network represented by the following adjacency matrix:
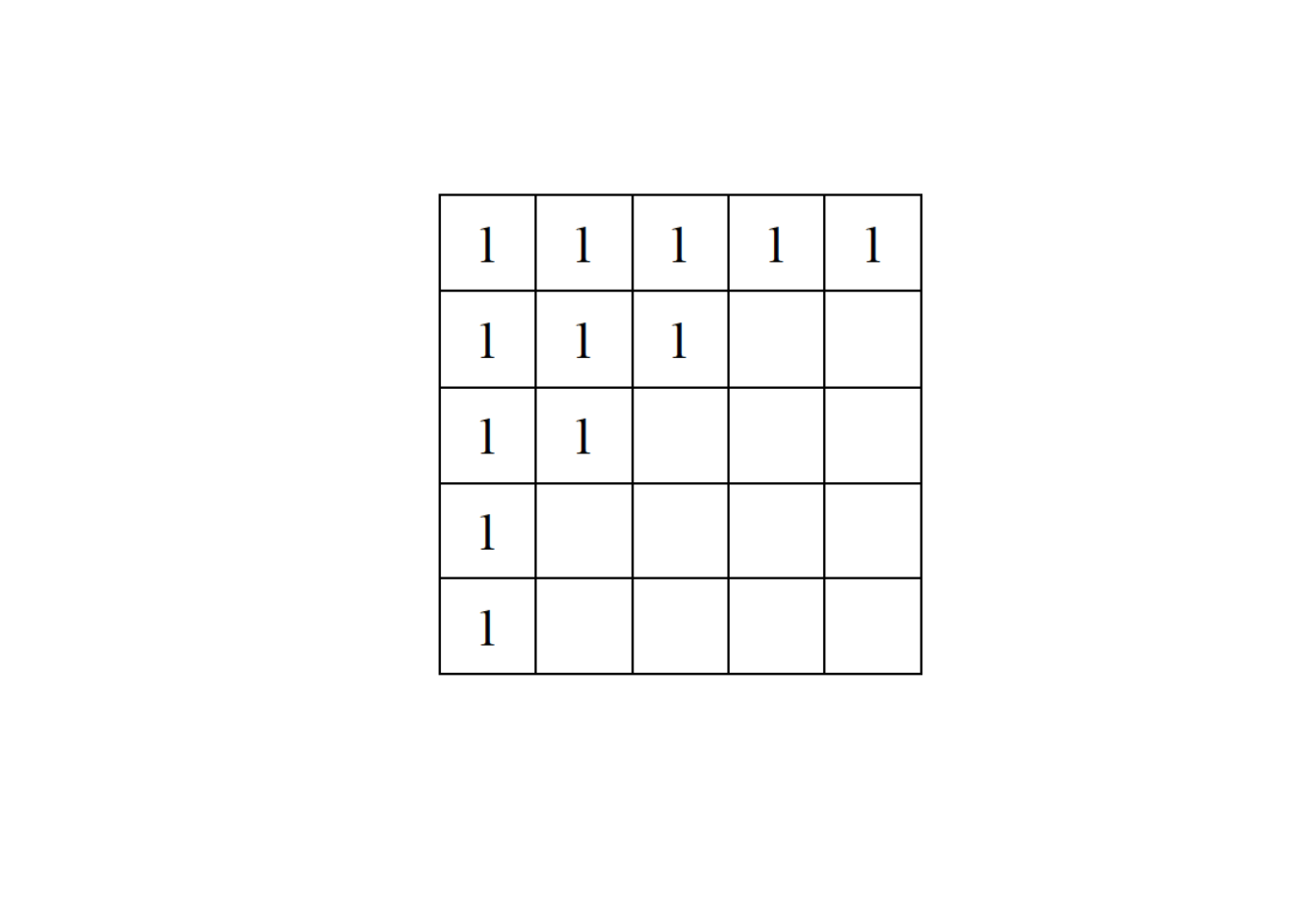
Provide a randomization of the matrix using:
a. the equifrequent null model
In your Rscript file, replace the ’x’s with the numbers you came up with in the randomization for the cell null model.
# -----------------------------------------------------------
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
# -----------------------------------------------------------b. the probabilistic cell null model
In your Rscript file, replace the ’x’s with the numbers you came up with in the randomization for the cell null model.
# -----------------------------------------------------------
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
# ------------------------------------------------------------ Consider now a second network represented by this adjacency matrix:
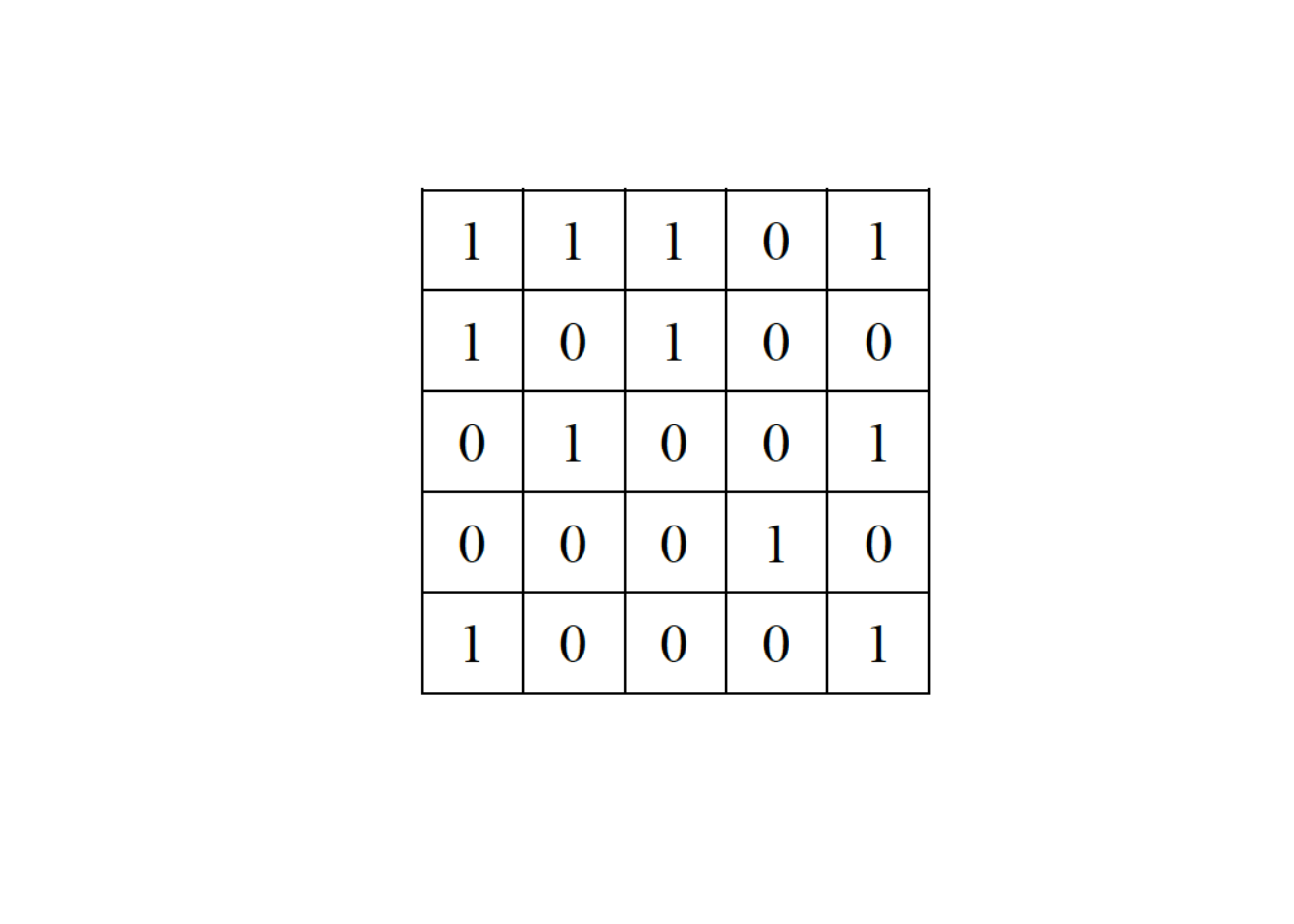
Provide three iterations of the swap algorithm:
first iteration
In your Rscript file, replace the ’x’s with the numbers you came up with in the randomization for the cell null model.
# -----------------------------------------------------------
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
# -----------------------------------------------------------second iteration
In your Rscript file, replace the ’x’s with the numbers you came up with in the randomization for the cell null model.
# -----------------------------------------------------------
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
# -----------------------------------------------------------third iteration
In your Rscript file, replace the ’x’s with the numbers you came up with in the randomization for the cell null model.
# -----------------------------------------------------------
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
#|-----------------------------------------------------------|
#| | | | | |
#| x | x | x | x | x |
#| | | | | |
# -----------------------------------------------------------5.2 Computer part I
In this section we will use R code to run the null models covered during this morning’s lecture. We will focus on using the null models to evaluate the nestedness value of a single network. Ultimately, we want to know if the measured nestedness value of our network is significantly different from the nestedness values obtained from a set of random iterations. To do this, we will first define a network and compute its nestedness. Then, we’ll compute nestedness again using the three null models we went over. Finally, we will estimate the significance of nestedness using the z-score.
Before we begin we should load the packages we will use for this session. Please note that we will use the rweboflife package to run the null models and compute nestedness.
# Load packages
library(igraph)
library(tidyverse)
library(bipartite)
# To install the rweboflife package, uncomment the following line and run it:
#devtools::install_github("bascompte-lab/rweboflife", force = TRUE)
# Load rweboflife package
library(rweboflife)5.2.1 Defining a network
For demonstration purposes, we will be using a perfectly nested network (10 rows x 10 columns) in this first part of the exercise. We begin by defining the network (stored as nested_mat) and visualising it.
# this function helps you to construct a perfectly nested matrix.
# As a arguments, you should specify the number of columns and rows.
perfect_nested <- function(my_cols, my_rows){
mat <- matrix(0, my_rows, my_cols)
for (i in seq(1,my_rows,1)) {
j_max <- ceiling(i*my_cols/my_rows)
# print(i)
# print(j_max)
# print("")
for (j in seq(1,j_max,1)) {
mat[i,j] <-1
}
}
return(t(mat))
}
# created the 10 x 10 perfectly nested matrix
nested_mat <- perfect_nested(10, 10)
# plot the matrix
visweb(nested_mat)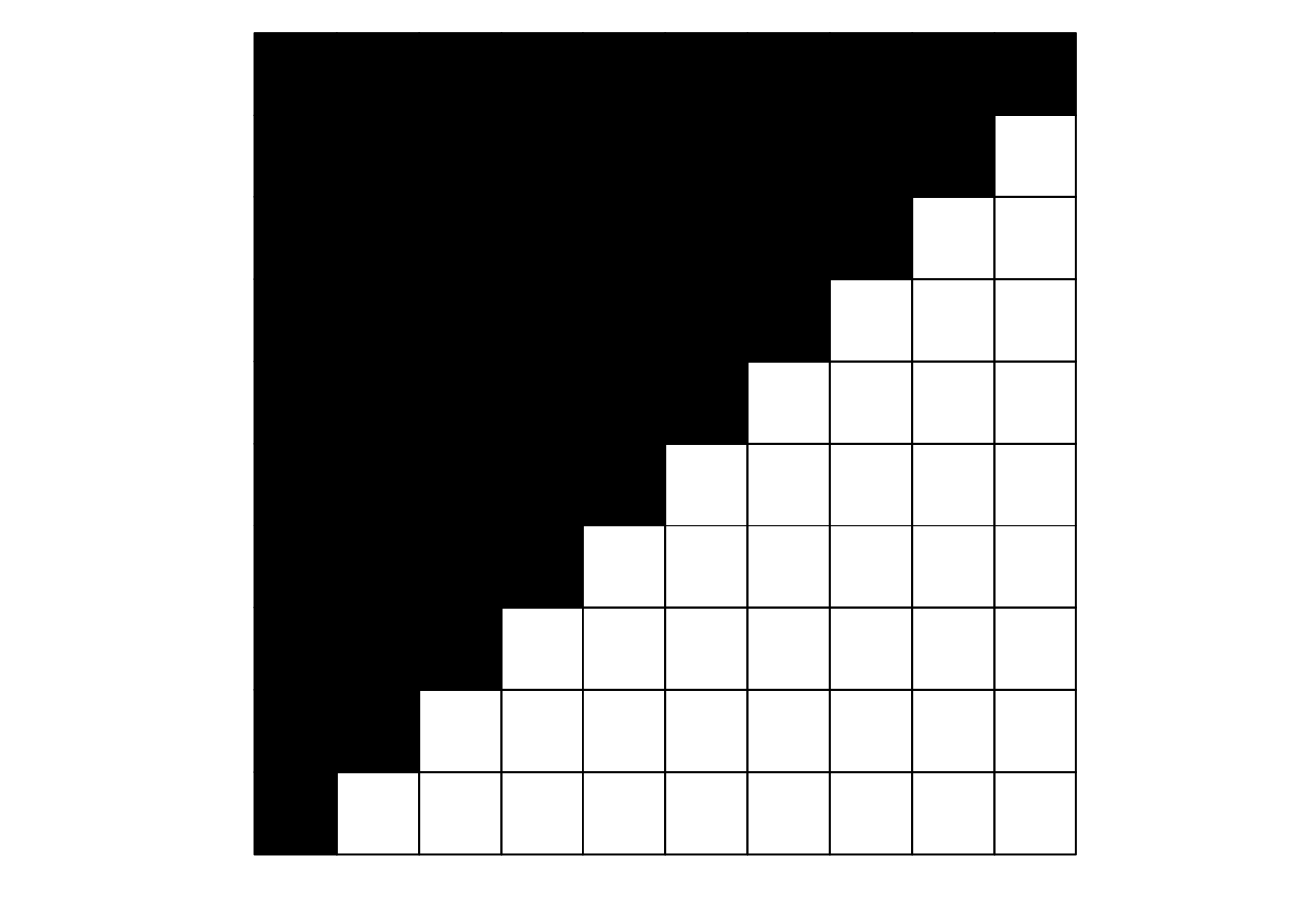
5.2.2 The nestedness function
Now that we have defined our network, we measure its nestedness. We will calculate nestedness using the function nestedness from the rweboflife package.
nestedness <- function(M){
# this code computes the nestedness of a given incident matrix M
# according to the definition given in
# Fortuna, M.A., et al.: Coevolutionary dynamics shape the structure of
# bacteria‐phage infection networks. Evolution 1001-1011 (2019).
# DOI 10.1111/evo.13731
# Make sure we are working with a matrix
M <- as.matrix(M)
# Binarize the matrix
B <- as.matrix((M>0))
class(B) <- "numeric"
# Get number of rows and columns
nrows <- nrow(B)
ncols <- ncol(B)
# Compute nestedness of rows
nestedness_rows <- 0
for(i in 1:(nrows-1)){
for(j in (i+1): nrows){
c_ij <- sum(B[i,] * B[j,]) # Number of interactions shared by i and j
k_i <- sum(B[i,]) # Degree of node i
k_j <- sum(B[j,]) # Degree of node j
if (k_i == 0 || k_j==0) {next} # Handle case if a node is disconnected
o_ij <- c_ij / min(k_i, k_j) # Overlap between i and j
nestedness_rows <- nestedness_rows + o_ij
}
}
# Compute nestedness of columns
nestedness_cols <- 0
for(i in 1: (ncols-1)){
for(j in (i+1): ncols){
c_ij <- sum(B[,i] * B[,j]) # Number of interactions shared by i and j
k_i <- sum(B[,i]) # Degree of node i
k_j <- sum(B[,j]) # Degree of node j
if (k_i == 0 || k_j==0) {next} # Handle case if a node is disconnected.
o_ij <- c_ij / min(k_i, k_j) # Overlap between i and j
nestedness_cols <- nestedness_cols + o_ij
}
}
# Compute nestedness of the network
nestedness_val <- (nestedness_rows + nestedness_cols) / ((nrows * (nrows - 1) / 2) +
(ncols * (ncols - 1) / 2))
return(nestedness_val)
}5.2.3 Computing nestedness
Let’s compute the nestedness value for the network we defined before, as in previous sessions. Next, we will implement the null models.
# Calculate the nestedness value for our network and store it
nestedness_perfectly_nested <- weboflife::nestedness(nested_mat)
nestedness_perfectly_nested## [1] 15.2.4 Equifrequent null model
First, we’ll start with the equifrequent null model. We can code the equifrequent model like this:
equifrequent_model <- function(M_in, iter_max){
rows <- nrow(M_in)
columns <- ncol(M_in)
number_ones <- count_nonzero(M_in)
count_ones <- 0
M_equif <- matrix(0, rows, columns)
while (count_ones < number_ones) {
x <- ceiling(runif(1, min = 0, max = rows))
y <- ceiling(runif(1, min = 0, max = columns))
while (M_equif[x,y] == 1) {
x <- ceiling(runif(1, min = 0, max = rows))
y <- ceiling(runif(1, min = 0, max = columns))
}
M_equif[x,y] <- 1
count_ones <- count_ones + 1;
}
return(M_equif)
}To run the equifrequent model, we will use the null_model from the rweboflife package. This function takes three arguments. 1) M_in specifies the matrix you wish to randomise and 2) model specifies the null model you wish to use to randomise the matrix (you can choose from: “equifrequent”, “cell” and “swap”) and 3) iter_max which determines how many iterations to run. To run the equifrequent model on the network we previously defined, we run the following command:
test_randomistion_equifrequent <- weboflife::null_model(M_in = nested_mat,
model = "equifrequent",
iter_max = 1)Now that we have randomised the matrix, we can compute the nestedness of this randomisation.
# Calculate the nestedness value for our network and store it
nestedness_test_randomistion_equifrequent <- weboflife::nestedness(
test_randomistion_equifrequent)
nestedness_test_randomistion_equifrequent## [1] 0.6066138The raw nestedness value differs between the empirical network and its randomisation. However, one single randomisation is not enough to draw a conclusion. Instead, we should perform several randomistations and compute the nestedness value of each one. Then, we can compare the nestedness value of the empirical networks with the distribution of nestedness values from our randomisations. Let’s generate 100 randomisations of our network and compute nestedness for each one.
# define number of randomisations
n <- 100
# run randomistations
nestedness_from_equifrequent <- replicate(n, weboflife::nestedness(
weboflife::null_model(M_in = nested_mat, model = "equifrequent",
iter_max = 1)), simplify=TRUE)Now that we have our nestedness estimates, we need to estimate the significance of the nested value we initially observed using the z-score. The formula to estimate z-scores is:
\[ z-score = \frac{observed\ nestedness - mean(nestedness)}{sd(nestedness)} \]
To calculate the z-score, we first have to obtain the mean and the standard deviation of the nestedness values we obtain from our null model. The mean and standard deviation are calculated in R with the mean and sd functions, respectively. Run the command below in your Rscript file, make sure to add the required parameter values.
# Compute mean for nestedness values estimated by null model
mean_nestedness <- mean()
# Compute sd for nestedness values estimated by null model
sd_nestedness <- sd()Now we can calculate the z-score for the null model. Run the command below in your Rscript file, make sure to add the required parameter values.
# Compute z score following formula
z_score <- Finally we can calculate the probability associated to the z-score using the pnorm and setting the lower.tail parameter to FALSE. Run the command below in your Rscript file, make sure to add the required parameter values.
# Compute associated p value
p_val <-pnorm(, lower.tail = FALSE)
# Print p value
print(p_val)5.2.5 Probabilistic cell model
Now let’s move to the probabilistic cell model. We can code the equifrequent model like this:
cell_model <- function(M_in, iter_max){
rows <- nrow(M_in)
columns <- ncol(M_in)
# binarize M_in
M <- as.matrix((M_in>0))
class(M) <- "numeric"
PR <- matrix(0, rows, 1)
PC <- matrix(0, columns, 1)
M_cell <- matrix(0, rows, columns)
for (i in 1:rows){
number_ones <- 0
for (j in 1:columns){
if(M[i,j] == 1){
number_ones <- number_ones + 1
}
}
PR[i] <- number_ones/columns
}
for (j in 1:columns){
number_ones <- 0
for (i in 1:rows){
if(M[i,j] == 1){
number_ones <- number_ones + 1
}
}
PC[j] <- number_ones/rows
}
for (i in 1:rows){
for (j in 1:columns){
p <- (PR[i]+PC[j])/2;
r <- runif(1)
if( r < p ){
M_cell[i,j] <- 1;
}
}
}
return(M_cell)
}Repeat the same process we followed for the equifrequent null model, but now using the probabilistic cell model. You should do the following:
- Run the null model 100 times using the
nested_mat. - Compute the mean and standard deviation of our null model estimates.
- Calculate the z-score.
- Obtain an associated p-value.
# Run the probabilistic cell model in your own Rscript5.2.6 Swap model
Lastly, we focus on the swap model. We can code the equifrequent model like this:
swap_model = function(M_in, iter_max){
nr <- nrow(M_in) # number of rows
nc <- ncol(M_in) # number of columns
# initialize M (randomized matrix) iter loop
M <- M_in
for(iter in 1:iter_max){
# binarize M into a logical matrix
B <- as.matrix((M>0))
# flatten logical matrix with row-major order
M_vec <- as.vector(t(B))
allEqual <- TRUE
while (allEqual == TRUE){
indexes <- create_indexes(nr, nc)
sub_vec <- M_vec[indexes]
allEqual <- xor(all(sub_vec), all(!(sub_vec)))
}
# shaffle indexes till all positions are swapped
fullRND <- FALSE
while (fullRND == FALSE){
indexes_rnd <- indexes[shuffle(indexes)]
fullRND <- all(indexes_rnd != indexes)
}
M_vec[indexes_rnd] <- sub_vec
M_swap <- matrix(M_vec, nrow=nr, ncol=nc, byrow=TRUE) # back to matrix
M <- M_swap
class(M_swap) <- "numeric"
}
return(M_swap)
}Repeat the same process we followed for the other two null models, but now using the swap model. You should do the following:
- Run the null model 100 times with using the
nested_mat. - Compute the mean and standard deviation of our null model estimates.
- Calculate the z-score.
- Obtain an associated p-value.
# Run the swap model in your own Rscript5.3 Computer part II
In this final section, we will use the null models to test whether a set of pollination networks are significantly more or less nested than a set of seed dispersal networks. We will use null models to answer this question.
5.3.1 Code
To save some time, I have already downloaded the necessary networks. The first thing we need to is to load the networks. The seed dispersal networks are stored as entries in the list called seed_networks which is found in the seed_networks.Rdata file. The pollination networks are stored as entries in the list called pollination_networks which is found in the pollination_networks.Rdata file. We will begin by loading these two files.
# Load pollination networks
load("~/ecological_networks_2023/downloads/Data/03-23_null_models/pollination_networks.Rdata")
# Load seed networks
load("~/ecological_networks_2023/downloads/Data/03-23_null_models/seed_networks.Rdata")Now that we have our networks, we can continue to run the null models, in this example we will use the cell null model. Let’s outline our workflow:
- First, compute the nestedness value of each of the networks in the
seed_networksandpollination_networkslists. - Next, perform 20 randomisations of each network using the cell null model.
- Finally, run a t-test to determine whether there are differences between the two types of networks in relation to their standardized nestedness values.
Below you will find the code to perform the workflow outlined above. However, if you’re up for a challenge, feel free to write your own code. Use the p-value you obtain to answer the question at the bottom of this exercise.
#################################################
# SEED DISPERSER NETWORKS
#################################################
# calculate nestedness value of empirical networks
seed_nestedness <- sapply(seed_networks, weboflife::nestedness)
# generate 20 randomisations of each seed dispersal network using the equifrequent model
seed_randomisations <- replicate(20, lapply(seed_networks, weboflife::null_model,
model = 'cell' ))
# compute the nestedness value of each randomisation
seed_randomisations_nestedness <- sapply(seed_randomisations, weboflife::nestedness)
# extract nestedness value of each randomisation
seed_randomisations_nestedness <- split(seed_randomisations_nestedness,
ceiling(seq_along(seed_randomisations_nestedness)/20))
# compute mean nestedness of each randomisation
mean_seed_randomisations_nestedness <- sapply(seed_randomisations_nestedness, mean)
# compute sd nestedness of each randomisation
sd_seed_randomisations_nestedness <- sapply(seed_randomisations_nestedness, sd)
# calculate z-score of each network
seed_z_score <- (seed_nestedness - mean_seed_randomisations_nestedness)/
sd_seed_randomisations_nestedness
#################################################
# POLLINATION NETWORKS
#################################################
# calculate nestedness value of empirical networks
pollination_nestedness <- sapply(pollination_networks, weboflife::nestedness)
# generate 20 randomisations of each seed dispersal network using the equifrequent model
pollination_randomisations <- replicate(20, lapply(pollination_networks,
weboflife::null_model,
model = 'cell'))
# compute the nestedness value of each randomisation
pollination_randomisations_nestedness <- sapply(pollination_randomisations,
weboflife::nestedness)
# extract nestedness value of each randomisation
pollination_randomisations_nestedness <- split(pollination_randomisations_nestedness,
ceiling(seq_along(pollination_randomisations_nestedness)/20))
# compute mean nestedness of each randomisation
mean_pollination_randomisations_nestedness <- sapply(pollination_randomisations_nestedness,
mean)
# compute sd nestedness of each randomisation
sd_pollination_randomisations_nestedness <- sapply(pollination_randomisations_nestedness,
sd)
# calculate z-score of each network
pollination_z_score <- (pollination_nestedness - mean_pollination_randomisations_nestedness)/
sd_pollination_randomisations_nestedness
#################################################
# COMPARE NETWORKS
#################################################
# Calculate t-test to compare vector of zscores
t.test(seed_z_score,pollination_z_score)##
## Welch Two Sample t-test
##
## data: seed_z_score and pollination_z_score
## t = -0.7027, df = 17.625, p-value = 0.4914
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.4311341 0.7145558
## sample estimates:
## mean of x mean of y
## 0.6255704 0.9838595