6 Statistical models
Matthew Barbour
session 25/03/2022
6.1 Setup
# load required libraries
## for statistical models section
library(car)
library(MASS)
library(lme4)
library(tidyverse)
library(cowplot)
library(RCurl)
library(dotwhisker)
library(piecewiseSEM)
library(vegan)
library(broom)
# library(rstanarm)
## additional packages for rarefaction section
library(bipartite)
library(plotly)
library(imager)
# set default plot theme to cowplot
theme_set(theme_cowplot())
# load data and functions to speed up computation
load("~/ecological_networks_2022/downloads/Data/03-25_statistical_models/rarefaction-exercise.Rdata")
load("~/ecological_networks_2022/downloads/Data/03-25_statistical_models/gall_network.Rdata")6.2 Rarefaction
I’ve already downloaded and cleaned all weighted networks from the Web of Life database. Now let’s check what the minimum number of individual links sampled is for these cleaned up networks.
# What is the minimum frequency of sampled links?
min_L.freq <- min(plyr::ldply(lapply(weighted_networks_clean, FUN = function(x) sum(x)))$V1)
min_L.freq## [1] 60# Let's rarefy all weighted network down to this minimum number of links.
L.rare <- min_L.freqFor the subsequent analyses, we are going to rarefy each network down to 60 sampled links before comparing them.
6.3 Rarefaction Functions
We have finished all the necessary data wrangling. Now we can move on to calculating rarefied properties of each network. To do so, we will use the following functions.
## Function to perform rarefaction
link_rarefaction <- function(network, network_function, sample_sizes, permutations){
# transform network into link samples
link_samples <- data.frame(links = apply(wide_network(network), 1, function(x) rep(names(x), x)))
# perform rarefaction, keeping track of links
sim_data <- list()
for(i in 1:length(sample_sizes)){
perm_list <- list()
for(j in 1:permutations){
# randomly sample 'sample_sizes' (without replacement) and store in a data frame
# repeat "permutations"
perm_list[[j]] <- sample_n(link_samples, size = sample_sizes[i], replace = FALSE) %>%
mutate(sample_size = sample_sizes[i],
perm = j)
}
sim_data[[i]] <- plyr::ldply(perm_list)
}
sim_df <- plyr::ldply(sim_data)
# aggregate simulation data
sum_sims <- sim_df %>%
group_by(links, sample_size, perm) %>%
summarise(frequency = n()) %>%
arrange(links, sample_size, perm) %>%
as.data.frame()
spread_sims <- spread(sum_sims, links, frequency, fill=0)
get_network_metrics <- c()
for(i in 1:dim(spread_sims)[1]){
network_tmp <- select(spread_sims, -sample_size, -perm)[i, ] %>%
gather(links, frequency) %>%
separate(links, into=c("rows", "columns"), sep="-") %>% # this is where "additional pieces discarded" warning comes in
filter(frequency > 0) %>% # remove unsampled species and interactions
pivot_wider(names_from = columns,
values_from = frequency,
values_fill = list(frequency = 0)) %>% # refill with zero to account for observed species, but not observed interactions; can cause issues if col(row)names of species contain "-"
column_to_rownames(var="rows") %>%
as.matrix()
get_network_metrics[i] <- do.call(network_function, args = list(network_tmp))
}
sim_properties <- data.frame(select(spread_sims, sample_size, perm), metric = get_network_metrics)
return(sim_properties)
}
# turn adjacency matrix into edge list (long format), but keep zeros
long_network <- function(network){
gather_network <- network %>%
rownames_to_column %>%
gather(columns, frequency, -rowname)
return(gather_network)
}
# make a wide network
wide_network <- function(network){
spread_network <- long_network(network) %>%
unite(col = interaction_id, rowname, columns, sep = "-") %>%
spread(interaction_id, frequency)
return(spread_network)
}
# calculate the number of species
no_species = function(network){
S <- nrow(network) + ncol(network)
return(S)
}
# calculate the number of unique links
no_links = function(network){
L <- sum(network > 0)
return(L)
}
# calculate connectance
connectance = function(network){
C <- no_links(network) / (nrow(network)*ncol(network))
return(C)
} 6.4 Example: Latitudinal Gradient in Rarefied Species Richness
As a warmup, let’s calculate rarefied species richness for only one network. For now, we will do this with a small number of permutations, but for your exercise you should increase this.
# example with species richness and small number of permutations for one network
link_rarefaction(network = weighted_networks_clean[[25]], # select the first network in our downloaded list
network_function = no_species,
sample_sizes = L.rare,
permutations = 10) # increase permutations to 100 for your exercises## sample_size perm metric
## 1 60 1 23
## 2 60 2 23
## 3 60 3 23
## 4 60 4 23
## 5 60 5 23
## 6 60 6 23
## 7 60 7 23
## 8 60 8 23
## 9 60 9 23
## 10 60 10 23Now let’s calculate rarefied species richness for each of our downloaded networks.
# example of calculating rarefied species richness for each network in the list
rarefied_list <- lapply(X = weighted_networks_clean,
FUN = function(x) link_rarefaction(network = x,
network_function = no_species,
sample_sizes = L.rare,
permutations = 10)) Now we gather the rarefied data into a nice data frame.
# gather rarefied data into a nice data frame
rarefied_df <- plyr::ldply(rarefied_list) %>%
rename(name = .id) %>%
left_join(., weighted_network_info) %>%
group_by(name, author, interaction_type, latitude) %>%
summarise_at(vars(metric), list(mean)) %>%
# rename metric to match the function used
rename(S.rare = metric)
# inspect data
rarefied_df## # A tibble: 95 × 5
## # Groups: name, author, interaction_type [95]
## name author interaction_type latitude S.rare
## <chr> <chr> <chr> <dbl> <dbl>
## 1 A_HP_001 Hadfield et all 2013 Host-Parasite 42 17.9
## 2 A_HP_002 Hadfield et all 2013 Host-Parasite 51.2 23.1
## 3 A_HP_003 Hadfield et all 2013 Host-Parasite 49 24.1
## 4 A_HP_004 Hadfield et all 2013 Host-Parasite 50.3 17.1
## 5 A_HP_005 Hadfield et all 2013 Host-Parasite 49.8 12.9
## 6 A_HP_006 Hadfield et all 2013 Host-Parasite 40.2 20
## 7 A_HP_007 Hadfield et all 2013 Host-Parasite 66.4 18.6
## 8 A_HP_008 Hadfield et all 2013 Host-Parasite 42.3 14.6
## 9 A_HP_009 Hadfield et all 2013 Host-Parasite 45 18.9
## 10 A_HP_010 Hadfield et all 2013 Host-Parasite 46.2 22.7
## # … with 85 more rowsLet’s plot the relationship between latitude and rarefied species richness.
# plot relationship between latitude and rarefied species richness
plot_S.rare_lat <- ggplot(rarefied_df, aes(x=latitude, y=S.rare)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ x + I(x^2), se=TRUE)
# make interactive
ggplotly(plot_S.rare_lat)It appears there is a negative relationship between species richness and latitude. Let’s fit a linear model to quantitatively examine this relationship.
# fit linear model
S.rare_lm <- lm(S.rare ~ latitude + I(latitude^2), rarefied_df)
# summarize model
summary(S.rare_lm)##
## Call:
## lm(formula = S.rare ~ latitude + I(latitude^2), data = rarefied_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.6544 -5.7914 -0.1869 4.3132 23.6252
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 24.5046877 1.4322179 17.110 <2e-16 ***
## latitude -0.1115733 0.0508591 -2.194 0.0308 *
## I(latitude^2) 0.0003294 0.0011013 0.299 0.7655
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.139 on 92 degrees of freedom
## Multiple R-squared: 0.111, Adjusted R-squared: 0.09165
## F-statistic: 5.742 on 2 and 92 DF, p-value: 0.004466This simple model suggests that there is a clear negative effect of latitude on species richness. Remember though, we haven’t accounted for other important covariates. For example, let’s check whether the negative effect of latitude is consistent across different interaction types.
# include interaction type
plot_S.rare_lat_type <- ggplot(rarefied_df, aes(x=latitude, y=S.rare, color = interaction_type)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ x, se=FALSE)
ggplotly(plot_S.rare_lat_type)We see that the apparent negative relationship with latitude is driven by the fact that many of the host-parasite networks in the dataset were sampled at high northern latitudes and these networks had comparatively low species richness. This emphasizes the important of visualizing and critically evaluating statistical models before making any scientific inferences.
6.5 Exercises
In the previous example, we used rarefaction to compare how a basic network property (species richness) varied across latitude. Importantly, we can use rarefaction to compare any network property we might be interested in. For this exercise, you’ll be applying what you’ve learned to study how connectance varies across latitude and whether results differ for rarefied vs. non-rarefied values.
1a. Plot the relationship between latitude and connectance (non-rarefied) for all weighted networks.
1b. Analyze the relationship between latitude and connectance.
Note that non-rarefied connectance has already been calculated and is labeled as C in the weighted_networks_info dataset.
2a. Calculate rarefied connectance for all weighted networks.
2b. Plot the relationship between latitude and rarefied connectance.
2c. Analyze the relationship between latitude and rarefied connectance.
3) Do you see different results for rarefied and non-rarefied connectance? If so, why do think this is?
4) Craving a challenge? Write your own network-property function (e.g. NODF) and see how this varies across latitude.
Note: This final part is not mandatory! You will not receive extra points.
6.7 Background
In this exercise, you will build a statistical model that predicts the frequency of trophic interactions in a food web. You’ll be using data from an experiment I conducted during my PhD (Barbour et al. 2016). I originally collected this data to study how genetic and phenotypic variation in plants affects the structure of their associated insect food web. The figure below will you give you a sense for what this food web looks like and how the data were collected. Please see Barbour et al. 2016 if you’re interested in more methodological details.
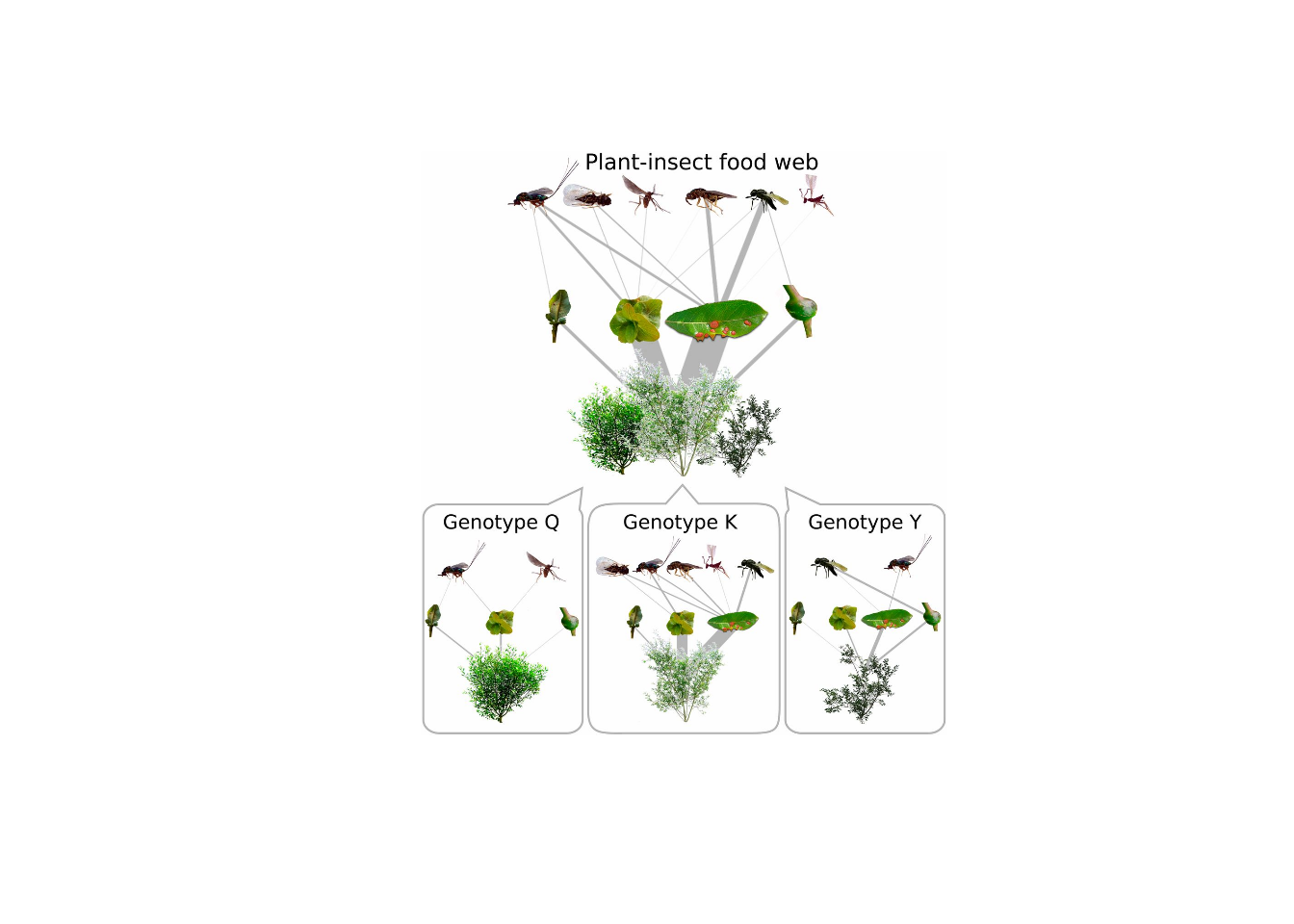
Figure 6.1: Genetic specificity of trophic interactions in a plant–insect food web. The species comprising the food web in this study include a host plant (coastal willow, Salix hookeriana), four herbivorous galling insects, and six insect parasitoids (species details in Materials and Methods of paper). The plant–insect food web consists of 16 trophic interactions (4 willow–gall and 12 gall–parasitoid) aggregated from all plant individuals sampled in this common garden experiment, whereas each genotype subweb represents the trophic interactions aggregated from all plant individuals of the corresponding genotype. We depicted three genotype subwebs (of 26) to illustrate the differences in trophic interactions associated with each willow genotype. The width of each gray segment is proportional to the number of individuals associated with each trophic interaction. Note that we scaled the width of trophic interactions to be comparable among genotype subwebs, but not between subwebs and the aggregated food web, to emphasize the differences among subwebs.
6.8 Data
Let’s download the data from my GitHub repository and prepare it for analysis. We need the data in “long” format for our statistical model.
# Download data from GitHub
gall_data <- read.csv(text=getURL("https://raw.githubusercontent.com/mabarbour/Genotype_Networks/master/manuscript/Dryad_data_copy/empirical_data/tree_level_interaxn_all_plants_traits_size.csv"), header=T)
## Tidy data for analysis ----
# Parasitoid interactions with *Iteomyia salicisverruca*
Iteomyia_data <- gall_data %>%
select(plant_genotype = Genotype, plant_ID = plant.position,
gall_abund = vLG_abund,
gall_size = vLG.height.mean,
Iteomyia_Platy = vLG_Platy,
Iteomyia_Mesopol = vLG_Mesopol,
Iteomyia_Tory = vLG_Tory,
Iteomyia_Eulo = vLG_Eulo,
Iteomyia_Mym = vLG_Mymarid) %>%
# never observed
mutate(Iteomyia_Lesto = 0) %>%
gather(link, frequency, -plant_genotype, -plant_ID, -gall_abund, -gall_size)
# Parasitoid interactions with *Rabdophaga salicisbrassicoides*
Rabdo.bud_data <- gall_data %>%
select(plant_genotype = Genotype, plant_ID = plant.position,
gall_abund = rG_abund,
gall_size = rG.height.mean,
Rabdo.bud_Platy = rG_Platy,
Rabdo.bud_Mesopol = rG_Mesopol,
Rabdo.bud_Tory = rG_Tory,
Rabdo.bud_Eulo = rG_Eulo,
Rabdo.bud_Lesto = rG_Lestodip) %>%
# never observed
mutate(Rabdo.bud_Mym = 0) %>%
gather(link, frequency, -plant_genotype, -plant_ID, -gall_abund, -gall_size)
# Parasitoid interactions with *Rabdophaga salicisbattatus*
Rabdo.stem_data <- gall_data %>%
select(plant_genotype = Genotype, plant_ID = plant.position,
gall_abund = SG_abund,
gall_size = SG.height.mean,
Rabdo.stem_Platy = SG_Platy) %>%
# never observed
mutate(Rabdo.stem_Mym = 0,
Rabdo.stem_Mesopol = 0,
Rabdo.stem_Tory = 0,
Rabdo.stem_Eulo = 0,
Rabdo.stem_Lesto = 0) %>%
gather(link, frequency, -plant_genotype, -plant_ID, -gall_abund, -gall_size)
# Parasitoid interactions with an undescribed gall midge species that
# forms an apical stem gall.
apical.stem_data <- gall_data %>%
select(plant_genotype = Genotype, plant_ID = plant.position,
gall_abund = aSG_abund,
gall_size = aSG.height.mean,
apical.stem_Tory = aSG_Tory) %>%
# never observed
mutate(apical.stem_Mym = 0,
apical.stem_Mesopol = 0,
apical.stem_Platy = 0,
apical.stem_Eulo = 0,
apical.stem_Lesto = 0) %>%
gather(link, frequency, -plant_genotype, -plant_ID, -gall_abund, -gall_size)
# bind everything into a long-format dataset
gall_long <- bind_rows(Iteomyia_data, Rabdo.bud_data, Rabdo.stem_data, apical.stem_data) %>%
separate(link, into = c("gall","parasitoid"), remove = FALSE, sep = "_") %>%
mutate(plant_ID = as.character(plant_ID))
# subset data so that gall_abund is greater than zero.
# this makes sense, because it is impossible to get an interaction otherwise
gall_long_sub <- filter(gall_long, gall_abund > 0)Now let’s inspect the data:
head(gall_long_sub) %>% arrange(plant_ID)## plant_genotype plant_ID gall_abund gall_size link gall
## 1 F 233 2 11.37 Iteomyia_Platy Iteomyia
## 2 * 240 4 6.90 Iteomyia_Platy Iteomyia
## 3 * 319 1 6.77 Iteomyia_Platy Iteomyia
## 4 * 329 1 8.73 Iteomyia_Platy Iteomyia
## 5 A 481 1 7.15 Iteomyia_Platy Iteomyia
## 6 * 87 1 7.09 Iteomyia_Platy Iteomyia
## parasitoid frequency
## 1 Platy 0
## 2 Platy 0
## 3 Platy 0
## 4 Platy 1
## 5 Platy 0
## 6 Platy 1Here is what each column in this dataset represents:
- plant_genotype: genetic identity of the plant (n = 25)
- plant_ID: individual identity of the plant (n = 116)
- gall_abund: number of gall species sampled from plant_ID (units = individuals per 5 branches sampled)
- gall_size: mean diameter of gall species from plant_ID (units = mm)
- link: unique gall-parasitoid interactions (n = 24)
- gall: gall species identity (short name, n = 4)
- parasitoid: parasitoid species identity (short name, n = 6)
- frequency: number of unique gall-parasitoid interactions sampled from plant_ID
6.9 Example
Note: I assume students have basic familiarity with interpreting statistical models in R. It is beyond the scope of this exercise to discuss all of the important details when building a statistical model. Instead, I focus on issues most relevant for modeling species-interaction networks. For those interested, I also provide code for applying Bayesian methods.
6.9.1 Build the model
Below I fit a simple statistical model to this data. It models the effect of gall and parasitoid species identity on the frequency of gall-parasitoid interactions. I assume the frequency of interactions follows a Poisson error distribution.
Note that I specified “sum contrasts” for the effect of gall and parasitoid species identity. This adjusts the coefficients so that they test the effect of a gall or parasitoid species relative to an imaginary “average” species. In other words, we now test whether species make above or below average contributions to food-web structure. I find this more informative than arbitrarily setting one species as the “baseline” and testing whether species contribute more or less than this baseline species.
gall_glm <- glm(frequency ~ gall + parasitoid,
data = gall_long_sub,
family = poisson(link="log"),
# 'contr.Sum' comes from the 'car' package, which
# I find more informative than 'contr.sum'
contrasts = list(gall = "contr.Sum",
parasitoid = "contr.Sum"))
## Bayesian with rstanarm
# exact same code as above. this uses default priors, which are designed to work well in many situations, but in practice, we should think carefully and specify our own.
# gall_stan_glm <- stan_glm(frequency ~ gall + parasitoid + link,
# data = gall_long_sub,
# family = poisson(link="log"),
# contrasts = list(gall = "contr.Sum",
# parasitoid = "contr.Sum"))6.9.2 Analyze the results
One useful summary statistic of our model is its R2, which indicates how much of the variance1 it explains in the data.
rsquared(gall_glm) ## Response family link method R.squared
## 1 frequency poisson log nagelkerke 0.331834## Bayesian
# bayes_R2(gall_stan_glm)
# but only available for Gaussian and binomial models, note that the Bayesian version is again different from a classic linear model.We see that the model explains 33% of the variance in gall-parasitoid interactions.
We can also test whether gall or parasitoid species identity have clear effects2 on the frequency of interactions.
# likelihood ratio test of gall and parasitoid species identity
drop1(gall_glm, test="LR")## Single term deletions
##
## Model:
## frequency ~ gall + parasitoid
## Df Deviance AIC LRT Pr(>Chi)
## <none> 823.54 1178.0
## gall 3 937.05 1285.5 113.51 < 2.2e-16 ***
## parasitoid 5 1025.65 1370.1 202.12 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Bayesian
# not quite an equivalent, but you can look at uncertainty in effect sizes to help decide whether dropping one factor would affect the model's predictions. You can also do a more formal comparison that uses leave-one-out cross-validation (loo) to compare models, but we won't go into that here.These tests indicate that the identity of both the gall and parasitoid species have clear effects on the frequency of interactions.
We can also go into more detail by looking at the effect of particular gall and parasitoid species.
summary(gall_glm)##
## Call:
## glm(formula = frequency ~ gall + parasitoid, family = poisson(link = "log"),
## data = gall_long_sub, contrasts = list(gall = "contr.Sum",
## parasitoid = "contr.Sum"))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.2971 -0.6689 -0.2992 -0.1338 6.5761
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.9575 0.2294 -12.892 < 2e-16 ***
## gall[S.apical.stem] -1.4505 0.3478 -4.170 3.05e-05 ***
## gall[S.Iteomyia] 1.1713 0.1541 7.603 2.90e-14 ***
## gall[S.Rabdo.bud] 0.1058 0.1749 0.605 0.545390
## parasitoid[S.Eulo] 0.2889 0.2497 1.157 0.247283
## parasitoid[S.Lesto] -1.3206 0.4111 -3.212 0.001317 **
## parasitoid[S.Mesopol] 1.0018 0.2208 4.538 5.68e-06 ***
## parasitoid[S.Mym] -2.9300 0.8380 -3.496 0.000472 ***
## parasitoid[S.Platy] 1.6133 0.2068 7.802 6.10e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 1139.17 on 1151 degrees of freedom
## Residual deviance: 823.54 on 1143 degrees of freedom
## AIC: 1178
##
## Number of Fisher Scoring iterations: 7## Bayesian
# summary(gall_stan_glm)The above summary is good for statistical details, but is not that intuitive. Instead, we can visualize the effects of gall and parasitoid species identity.
# plot effect of gall and parasitoid species.
# errors bars represent 95% confidence intervals.
# the dotted line is placed at an imaginary "average" species.
# now you can interpret species as having above or below average effects.
dwplot(gall_glm) + geom_vline(xintercept = 0, linetype = "dotted")
## Bayesian
# plot(gall_stan_glm, prob = 0.66, prob_outer = 0.95)This plot shows that certain gall and parasitoid species have above and below average effects on the frequency of interactions. In other words, species vary in their contributions to food-web structure.
6.9.3 Assessing model fit
Is there room for improving the model? We can gain more insight by visualizing how well this statistical model predicts the observed frequency of interactions.
gall_long_sub %>%
# add predictions to the data
mutate(Predicted = fitted(gall_glm)) %>%
# plot the data
ggplot(., aes(x=frequency, y=Predicted)) +
geom_point() +
geom_abline(slope = 1, intercept = 0) +
xlab("Observed")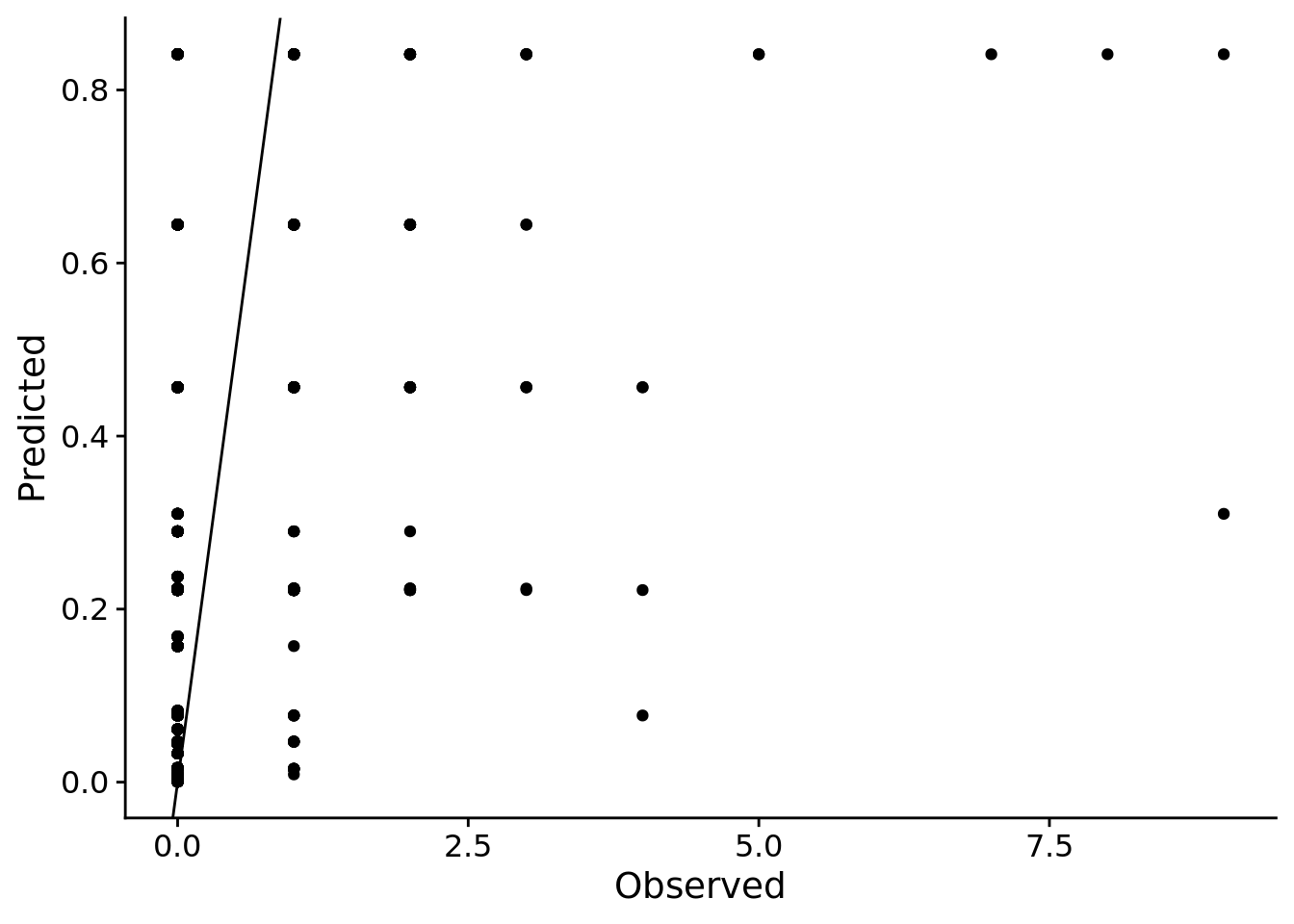
## Bayesian
# you can do the same as above, just replace 'gall_glm' with 'gall_stan_glm', or for a similar plot:
# pp_check(gall_stan_glm) # zoom in if you'd like by adding + coord_cartesian(xlim = c(0,3))Ideally, all points would be around the 1:1 line, indicating that our model predictions match our observations. Instead, it appears our model predicts that interactions are less frequent than what we usually observed (i.e. most observations fall below the 1:1 line). This is likely because there are a lot of zeros in the dataset, which could make a Poisson error distribution a bad choice.
The plot above is good for giving an overall picture of our model fit, but it doesn’t give us a sense for how good it is at predicting the observed composition of interactions (i.e. frequency of the 24 unique gall-parasitoid interactions). Below, I give an example of how we can simulate the composition of interactions predicted by our model and see how well they match our observations.
# choose the number of times you want to simulate
# the composition of interactions
nsims <- 100
# simulate and organize data
sim_df <- bind_cols(select(gall_long_sub, plant_ID, gall, parasitoid, frequency),
# simulation
# Bayesian? replace with:
#data.frame(t(posterior_predict(gall_stan_glm, draws = nsims)))) %>%
simulate(gall_glm, nsim = nsims)) %>%
unite(id, gall, parasitoid, sep = "-") %>%
gather(type, values, -plant_ID, -id) %>%
spread(id, values, fill=0) %>%
select(-plant_ID) %>%
# summarise across plants
group_by(type) %>%
summarise_all(list(sum)) %>%
ungroup() %>%
mutate(type = ifelse(type == "frequency", "obs", "sim"))
# principal components analysis to represent the composition of interactions
comp <- vegan::decostand(select(sim_df, -type), method = "hellinger")
sim_pca <- vegan::rda(comp ~ 1, data = sim_df)
# plot the observed vs. simulated composition of interactions in two dimensions
plot(sim_pca, type="n")
points(sim_pca, dis="sites",
pch=ifelse(sim_df$type == "sim", 1, 21),
bg=ifelse(sim_df$type == "sim", "grey", "black"),
col=ifelse(sim_df$type == "sim", "grey", "black"))
title(main = "Composition of species interactions")
It looks like this model does a pretty poor job at predicting the composition of interactions (we are aiming for a bullseye). Note that this is a simulation, so re-running the code above will change the plot (feel free to also modify the number of simulations nsims).
It is still difficult to interrogate the modeled composition of interactions with the above plot. Below, I’ve come up with an alternative visualization. Here, we look at how well our model predicts the average frequency of each gall-parasitoid interaction.
# get average frequency of observed and predicted links
# across all plants
fitted_composition_df <- gall_long_sub %>%
mutate(Predicted = fitted(gall_glm)) %>% # Bayesian? replace with: fitted(gall_stan_glm)
group_by(link, gall, parasitoid) %>%
summarise_at(vars(frequency, Predicted), list(mean = mean)) %>%
arrange(frequency_mean)
# sort links by their observed frequency. I think this
# helps make the plot more informative
fitted_composition_df$link <- factor(fitted_composition_df$link, levels = unique(fitted_composition_df$link))
# plot observed vs. predicted composition
ggplot(fitted_composition_df, aes(x = link, y = frequency_mean, color = "Observed")) +
geom_segment(aes(xend = link, y = frequency_mean, yend = Predicted_mean, color = "Predicted"), arrow = arrow(length = unit(0.2,"cm"))) +
geom_point() +
scale_color_manual(values = c("black","steelblue"), name = "") +
coord_flip()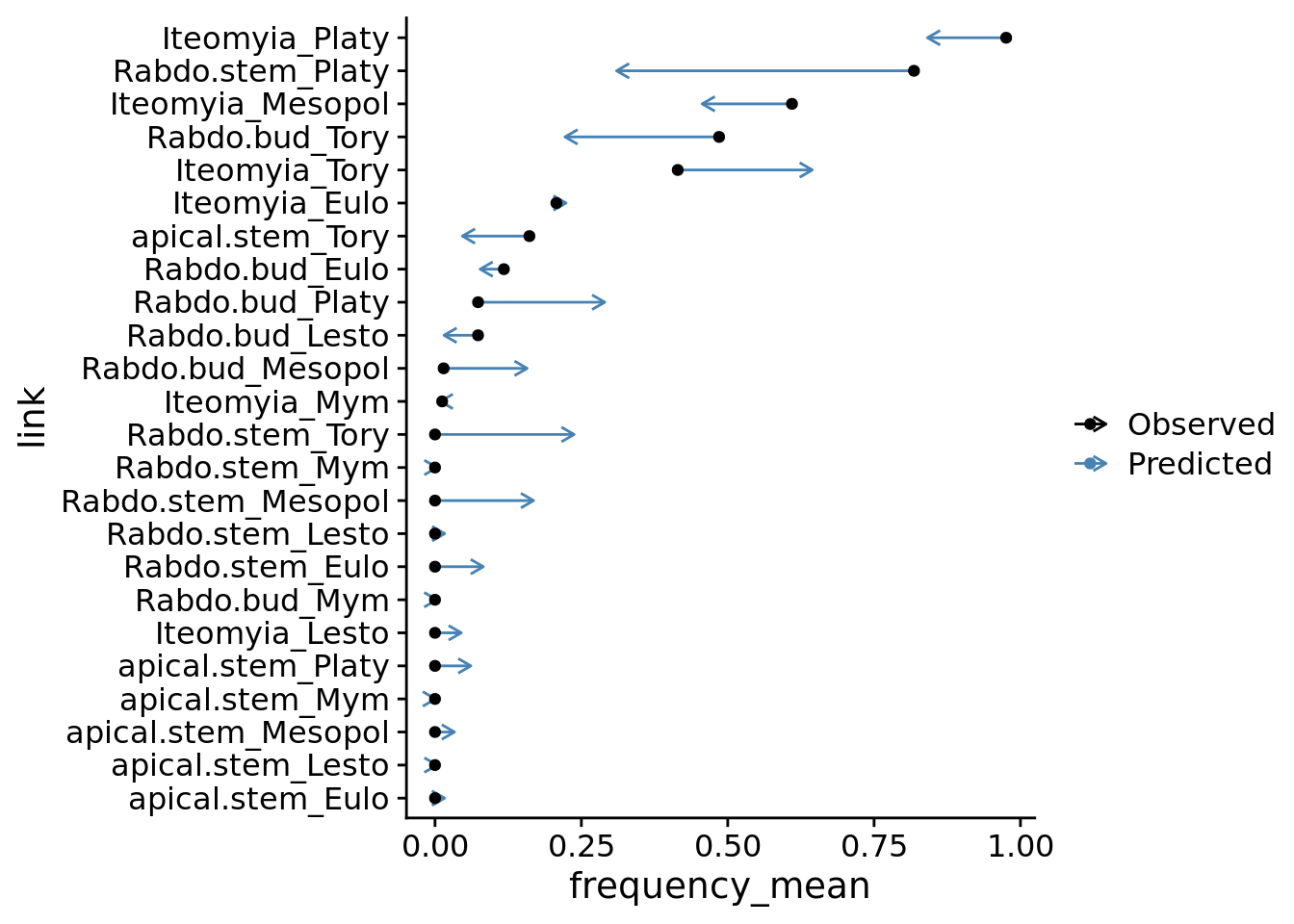
Inspecting the above plot, you can see the model under (e.g. Rabdo.stem_Platy) and over predicts (e.g. Iteomyia_Tory) certain gall-parasitoid interactions. This could indicate that there is specialization in gall-parasitoid interactions that is not captured by our current model.
Finally, we can examine how well our model does at reproducing aggregate properties of the network that we may be interested in, such as connectance.
## Example: Examine how well your model reproduces network connectance
# function to calculate the number of links
no_links = function(network){
L <- sum(network > 0)
return(L)
}
# function to calculate connectance
connectance = function(network){
C <- no_links(network) / (nrow(network)*ncol(network))
return(C)
}
# for loop to get connectance for the simulated networks
get_connectance <- c()
for(i in 1:dim(sim_df)[1]){
network_tmp <- select(sim_df, -type)[i, ] %>% # Bayesian? no change needed, because sim_df is from previous code
gather(links, frequency) %>%
separate(links, into=c("rows", "columns"), sep="-") %>%
filter(frequency > 0) %>% # remove unsampled species and interactions
spread(columns, frequency, fill=0) %>% # refill with zero to account for observed species, but not observed interactions
column_to_rownames(var="rows") %>%
as.matrix()
get_connectance[i] <- connectance(network_tmp)
}
# organize data
sim_properties <- data.frame(select(sim_df, type), C = get_connectance)
# plot observed vs. simulated connectance
sim_properties %>%
filter(type != "obs") %>%
ggplot(., aes(x=type, y=C)) +
geom_boxplot(outlier.shape = NA) +
geom_jitter(shape=1, height=0, width=0.1, color="grey") +
geom_point(data = filter(sim_properties, type == "obs"), size=3) +
ylab("Connectance")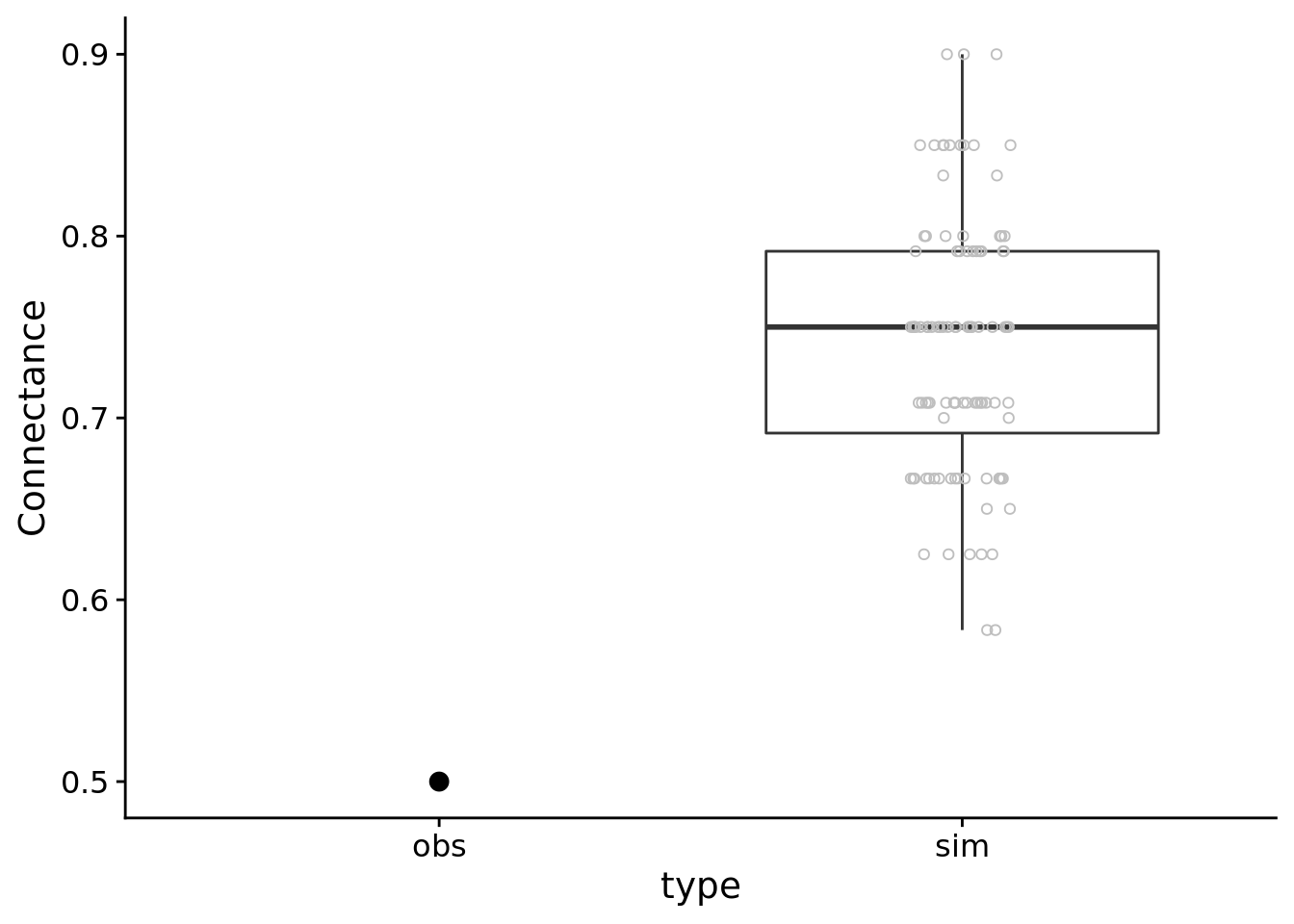
It looks like the model predicts a more connected network than we observed in the data. One possible explanation for this pattern is that we did not model a statistical interaction between the gall and parasitoid species (e.g. + gall:parasitoid). If this statistical interaction is important, it would indicate that parasitoids specialize in attacking certain gall species, which could result in a less connected network.
Note that you could substitute connectance for any aggregate network property you are interested in. This allows us to directly assess how our statistical model of species interactions shapes network structure. This is simply not possible with a null modeling approach.
6.10 Exercises
1) Build a statistical model that explains the frequency of gall-parasitoid interactions.
Explore the data and build a new model that is different from the one I gave in the example. Go at your own pace. Add complexity to satisfy your own curiosity. A more complex model does not mean a higher grade! You goal should be to come up with a better model than the example one.
Things to consider adding or changing from the example model:
- Add interaction between resource and consumer identities (e.g.
+ gall:parasitoid, if you do it may be a good idea to use Bayesian methods3) - Add sampling effort (e.g.
+ gall_abund) - Add traits (e.g.
+ gall_size) - Change error distribution (e.g. negative binomial with
glm.nb()function) - Mixed-effect model (e.g. add random intercept with
glmer()function:(1 | plant_genotype)and/or(1 | plant_ID); usestan_glmer()if you are using Bayesian methods)
2) Analyze the model. See previous example for suggestions on how to analyze the model.
3) Assess model fit. See previous example for suggestions on how to assess model fit.
4) In what ways did your model improve upon the example? Why do you think these improvements resulted in a better fit to the data?
5) Write down your own multiple choice question related to the topics covered today (during the lecture or exercise session). This can be related to either rarefaction or statistical models. Provide one correct answer and two incorrect answers.
Note that R2 does not have the same exact meaning as in a linear model. Still, it can be a useful summary statistic for a model. See Nakagawa and Schielzeth 2012 for a useful introduction.↩︎
I prefer using the term “clear” instead of “significant” or “statistically significant”. It’s more concise and a more accurate indication of what a P-value actually is (Dushoff et al. 2019). In fact, you should never use P < 0.05 to make a scientific conclusion. Read Wasserstein et al. 2019 for practical guidance.↩︎
You’ll run into issues of numerically fitted rates (very large or zero), because some species were never observed to interact. This causes issues with typical glms, but is handled better with Bayesian methods.↩︎