7 Assessing topological robustness

Alessandro Vindigni
session 29/03/2022

In the introductory lecture held by Prof. Bascompte you reviewed differences between random graphs (with a degree distribution showing a maximum) and scale-free networks. Among other aspects these two classes of networks react differently to random or systematic attack. Since the seminal work of Albert-Barabasi (2000) this approach has been used in many context to assess the topological robustness of a network. We use the adjective topological to distinguish this type of robustness from the resilience associated with the dynamics of a population.

The original study of Albert-Barabasi focused on unipartite networks. Here we consider a generalization of this approach to mutualistic networks that – as you should know by now – are bipartite.
The most natural way to assess this type of robustness is by progressively removing species of one guild and record the number of species of the other guild that remain without links. We further assume that species that are disconnected at a given stage of the simulation go extinct. For instance, for pollination networks this means that a plant goes extinct when it is left without pollinators a or, conversely, an insect goes extinct when it is left without resources.

In particular, within the chosen guild, species are removed following three different strategies

RND random removal
MTL systematic removal from most to least connected species (from generalist to specialist)
LTM systematic removal from least to most connected species (from specialist to generalist)

Typically, one plots the fraction of species of the second guild (e.g. plants) that goes extinct as a result of the removal of species of the primary guild (e.g. animals). We call the resulting diagram secondary extinction curve The following plot displays the secondary extinction curve obtained for the network M_PL_015 of the Web of life database.

annotation_MTL <- data.frame(
  x = 0.55,
  y = 0.75,
  label = "MTL"
)
annotation_LTM <- data.frame(
  x = 1.,
  y = 0.75,
  label = "LTM"
)
annotation_RND <- data.frame(
  x = 0.8,
  y = 0.75,
  label = "RND"
)

ggplot() +
  ggtitle(paste0("experiments M_PL_015")) +
  geom_point(data = filter(df_exp_example, strategy=="RND", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)), 
             color = "black",shape = 1) +
  geom_point(data = filter(df_exp_example, strategy=="LTM", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)),
             color = "dark green",shape = 1) +
  geom_point(data = filter(df_exp_example, strategy=="MTL", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)),
             color = "red",shape = 1) +
  xlab(TeX("$f_{rows}$")) +
  ylab(TeX("$f_{columns}$")) +
  # # Add text
  geom_text(data=annotation_LTM, aes( x=x, y=y, label=label),                  
            color="dark green", 
            size=4 , angle=0) +
  geom_text(data=annotation_MTL, aes( x=x, y=y, label=label),                  
            color="red", 
            size=4 , angle=0) +
  geom_text(data=annotation_RND, aes( x=x, y=y, label=label),                  
            color="black",
            size=4 , angle=0)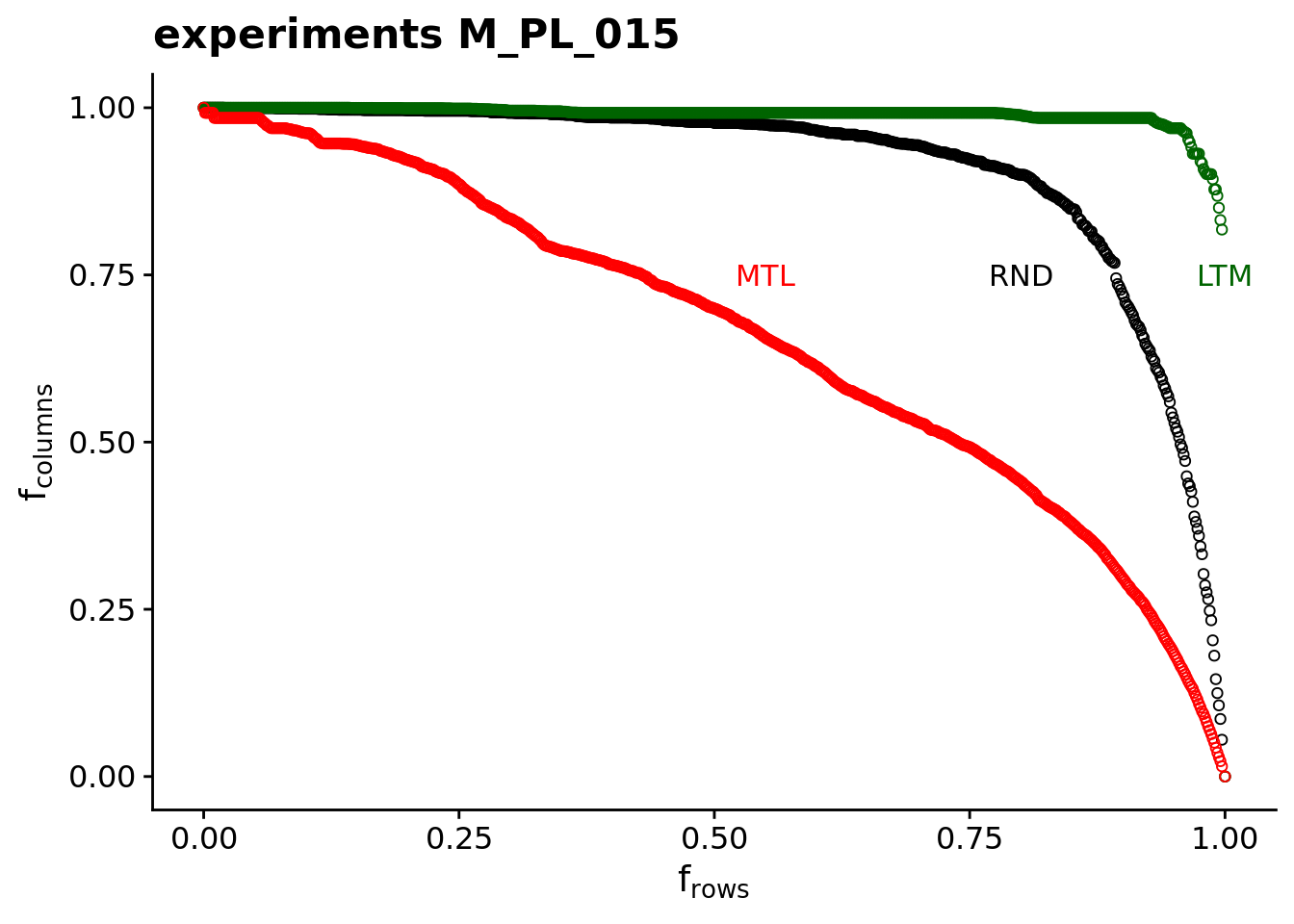

Your tasks

In the first stage of this exercise session you will use a function that in provide you to compute secondary extinction curves for four different pollination networks.
In the second stage you will repeat the same calculation for an idealized network characterized by a perfectly nested incidence matrix and compare it with the secondary extinction curves obtained for a selected experimental network.
In the third stage you will visualize the incidence matrix of a selected experimental network and compare it against its idealized counterpart of the same size.
In the forth stage you will remove some links at random from the perfectly nested incidence matrix and compare the resulting secondary extinctions curves with that of a perfectly nested network and with the selected experimental one.

Most of your tasks consist in understanding chunks of code that are given (but not executed!) and copy them into the R file you will submit. In this process, you will have to determine some parameters (like the matrix size) that are needed to display the secondary extinction curves in a standardized way.
I will pose few conceptual questions that you can answer as comments in the R script.

7.1 Secondary extiction curves

We consider the 4 pollination bipartite networks available on Web of life M_PL_015, M_PL_044, M_PL_054, M_PL_056. Let start downloading the network M_PL_015 (see session 03-17_toolkit_network_analysis):

base_url <- "https://www.web-of-life.es/"  

my_nw_name <- "M_PL_015" # "M_PL_044" # "M_PL_054" # "M_PL_056"
json_url <- paste0(base_url,"get_networks.php?network_name=",my_nw_name)
my_nw <- jsonlite::fromJSON(json_url)

# select the 3 relevant columns and create the igraph object 
my_graph <- my_nw %>% select(species1, species2, connection_strength) %>% 
  graph_from_data_frame() 

my_inc_mat <- incidence_matrix_from_graph(my_graph)

# you may compare the dimensions of this matrix with the number of species on the web interface 
dim(my_inc_mat)

## [1] 666 131

We can now use the function remove_rows(bipartite_network, n_iter, strategy, i_seed) to compute secondary extinction curves for the three removal strategies defined above. The function takes the following arguments:

bipartite_network: incidence matrix of the bipartite network
iter: integer number defining how many times the removal loop is repeated following different randomized sequences (iterations)
strategy: character “RND”, “MTL”, “LTM” defining the removal strategy
i_seed: integer, seed of the random sequence.

Not that this function treats the rows of the incidence matrix as the guild from which species are removed and columns as species that undergo secondary extinction. It is up to the user to pass the matrix with rows and columns ordered in the desired way.

The datasets of the simulated secondary-extinction curves for the network M_PL_015 are produced by the following code:

iterations <- 15
strategy_vec <- c("RND","MTL","LTM")
df_exp <- NULL
for(removal_strategy in strategy_vec){
  df_exp <- rbind(df_exp, remove_rows(my_inc_mat, iterations, removal_strategy, 645) %>%
                mutate("network_name" = my_nw_name, "strategy" = removal_strategy))
}

It is good practice to have a look at the dataframe (remove head() in your script)

formattable(head(df_exp))

7.1.1 Four pollination networks

Repeat the calculation for the networks M_PL_044, M_PL_054, M_PL_056 WITHOUT intializing again the dataframe df_exp <- NULL, namely progressively appending new rows

my_nw_name <- "M_PL_044" # "M_PL_054" # "M_PL_056"

#
#  repeat the commands that are needed to download data and produce the corresponding incidence matrix
#

iterations <- 15
strategy_vec <- c("RND","MTL","LTM")

for(removal_strategy in strategy_vec){
  df_exp <- rbind(df_exp, remove_rows(my_inc_mat, iterations, removal_strategy, 645) %>%
                mutate("network_name" = my_nw_name, "strategy" = removal_strategy))
}

Basically the chunk of code above needs to be repeated three times, one fore each network, the different datasets being identified by the column network_name in the dataframe df_exp.
Check if the dataframe contains the data you wanted to produce.

formattable(df_exp)

Task

If the data in the dataframe df_exp was properly computed, you should be able to produce the secondary extinction curves associated with the four pollination networks running the four scripts below. As in the example given above, data points should fall in the box from 0 to 1 both in the horizontal and in the vertical axis (double check the normalization of rows and columns if you notice something strange).
For each plot specify whether the horizontal axis \(f_{rows}\) corresponds to the fraction of removed plants or animals.

ggplot() +
  ggtitle(paste0("experiments M_PL_015")) +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)), 
             color = "black",shape = 1) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)),
             color = "dark green",shape = 1) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_015"), aes(removed_rows/666, (1- removed_columns/131)),
             color = "red",shape = 1) +
  xlab(TeX("$f_{rows}$")) +
  ylab(TeX("$f_{columns}$"))

ggplot() +
  ggtitle(paste0("experiments M_PL_044")) +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_044"), aes(removed_rows/609, (1- removed_columns/110)), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_044"), aes(removed_rows/609, (1- removed_columns/110)),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_044"), aes(removed_rows/609, (1- removed_columns/110)),
             color = "red",shape = 2) +
  xlab(TeX("$f_{rows}$")) +
  ylab(TeX("$f_{columns}$"))

ggplot() +
  ggtitle(paste0("experiments M_PL_054")) +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/113)), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/113)),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/113)),
             color = "red",shape = 2) +
  xlab(TeX("$f_{rows}$")) +
  ylab(TeX("$f_{columns}$"))

ggplot() +
  ggtitle(paste0("experiments M_PL_056")) +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_056"), aes(removed_rows/365, (1- removed_columns/91)), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_056"), aes(removed_rows/365, (1- removed_columns/91)),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_056"), aes(removed_rows/365, (1- removed_columns/91)),
             color = "red",shape = 2) +
  xlab(TeX("$f_{rows}$")) +
  ylab(TeX("$f_{columns}$"))

If you want to improve the appearance you could increase the number of iterations for a given strategy.
You can simply remove the dataset corresponding to a networks, e.g. M_PL_056, form the dataframe df_exp running the following command

df_exp <- filter(df_theo, network_name!="M_PL_056")

Question

After having produced the plots above, you will notice that all secondary extinction curves show a qualitatively similar behavior with respect to the different strategies in which nodes are removed: The curves associated with the strategies MTL and LTM have opposite concavity, while the curve obtained following the RND strategy lies between the other two curves. Explain with your words the reason for this observation.

7.2 Perfectly nested network

In this section we would like you to select one of the four pollination networks studied above and plot the secondary extinction curves obtained by removing animals (if you have not already computed them).
Select the network and produce the incidence matrix

my_nw_name <- # "M_PL_015" # "M_PL_044" # "M_PL_054" # "M_PL_056"
json_url <- paste0(base_url,"get_networks.php?network_name=",my_nw_name)
my_nw <- jsonlite::fromJSON(json_url)

# select the 3 relevant columns and create the igraph object 
my_graph <- my_nw %>% select(species1, species2, connection_strength) %>% 
  graph_from_data_frame() 

my_inc_mat <- incidence_matrix_from_graph(my_graph)

Since the function remove_rows() acts removing rows of the incidence matrix, you should check if animal species actually correspond to rows with the following command

rownames(my_inc_mat)

Should this not be the case, you need to transpose your matrix

my_inc_mat <-t(my_inc_mat)

and compute the secondary extinction curve again.

We now create a matrix, with the same number of rows and columns as the chosen experimental network, that is perfectly nested

nested_mat <- perfect_nested(nrow(my_inc_mat), ncol(my_inc_mat))

Expressed in this data structure the matrix nested_mat is suitable to be visualized (see next section). However, to pass it as an argument to the function remove_rows() we first need to convert it into a dataframe and assign some names to its rows and columns. I wrote the function species_df_from_matrix() that does this for you:

# convert to a format that can be passed to remove_rows()  
dim(nested_mat)
nested_df <- species_df_from_matrix(nested_mat)
dim(nested_df)

As you can see, the dataframe nested_df has the same dimensions as the original matrix.
We proceed computing the secondary extinction curve for this incidence matrix

my_nw_name <- "perfectly nested" 
strategy_vec <- c("RND","MTL","LTM")
conn <- as.double(sum(nested_mat))/(ncol(nested_mat)*nrow(nested_mat))

# innitialize the dataframe 
df_theo <- NULL

for(removal_strategy in strategy_vec){
  iterations <- 2
  if(removal_strategy=="RND") iterations <- 15
  
  df_theo <- rbind(df_theo, remove_rows(nested_df, iterations, removal_strategy, 645) %>%
                     mutate("network_name" = my_nw_name, 
                            "strategy" = removal_strategy, 
                            "connectance" = conn))
}

Let us have a look at the data we have computed

df_theo %>% formattable()

If we are satisfied we can proceed and plot our results, otherwise we can run the simulation again (e.g., increasing the number of iterations).

Task

Plot the secondary extinction curves obtained for the perfectly nested network and compare them against the same curves obtained for the chosen experimental network. This should be done simply running the following scripts, slightly modifying them:
Replace M_PL_054 with the name of the network you have chosen and adjust the actual number of rows and columns of the two incidence matrices to normalize the plot properly.

ggplot() +
  ggtitle(paste0("perfectly nested vs M_PL_054")) +
  geom_line(data = filter(df_theo, strategy=="RND",network_name=="perfectly nested"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))), 
            color = "black") +
  geom_line(data = filter(df_theo, strategy=="LTM",network_name=="perfectly nested"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green") +
  geom_line(data = filter(df_theo, strategy=="MTL",network_name=="perfectly nested"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))),
            color = "red",linetype = "dotted") +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_054"), aes(removed_rows/318, (1- removed_columns/ncol(my_inc_mat))),
             color = "red",shape = 2) +
  ylab(TeX("$f_{plants}$")) +
  xlab(TeX("$f_{animals}$"))

Questions

What are the main differences between the secondary extinction curves obtained for the two networks (incidence matrices)?
How can you explain the behavior of the secondary extinction curves obtained for the perfectly nested network following the systematic removal strategies LTM and MTL?

7.3 Visualize incidence matrices

In this section we provide you the commands to visualize both the experimental and the perfectly nested network. Obviously the connectance of the two matrices is not comparable. We can make the perfectly nested network more akin to the experimental one by removing some links at random till we have reached a predefined nominal density of links (nominal connectance). We provide the function diluted_matrix() that does this.

Task

Visualize the incidence matrix associated with the perfectly nested network, with the chosen pollination network, and with a diluted perfectly nested network and save every figure in the folder AssignmentMailbox/03-29_assessing_topological_robustness:
from the tab Plots, click on Export > Save as Image.

As an example we show you how a checkerboard matrix is visualized

library('plot.matrix')
# checker board example
checkerboard<- matrix(rep(c(1,0,1,0,1,0,1,0,1,0),24), ncol=23) 
plot(checkerboard, key=NULL, border=NA,  col.ticks=NA, # cex.axis=NA,
     col=c('light grey','blue'), breaks=c(0, 0.5, 1))

Similarly you can visualize and save your perfectly nested matrix

plot(nested_mat, key=NULL, border=NA,  col.ticks=NA, # cex.axis=NA,
     col=c('light grey','blue'), breaks=c(0, 0.5, 1))

and the incidence matrix of the experimental network.

dim(my_inc_mat)
my_inc_mat_ordered <- my_inc_mat[,order(colSums(my_inc_mat))]
colnames(my_inc_mat_ordered) <- NULL
rownames(my_inc_mat_ordered) <- NULL

plot(my_inc_mat_ordered, key=NULL, border=NA,  col.ticks=NA, # cex.axis=NA,
     col=c('light grey','blue'), breaks=c(0, 0.5, 1))

In this example we dilute the perfectly nested matrix till only 20% of the links are nominally left (using the function diluted_matrix()).

# leave roughly 0.2 of the possible links  
perc_links <- 0.2
diluted_mat <- diluted_matrix(nested_mat, perc_links)
dim(diluted_mat)

Visualize the diluted matrix obtained in this way and save it in the same location as the other two images.

plot(diluted_mat, key=NULL, border=NA,  col.ticks=NA, # cex.axis=NA,
     col=c('light grey','blue'), breaks=c(0, 0.5, 1))

7.4 Diluted incidence matrices

It is interesting at this point to compute secondary extinction curves for different degree of dilution of the perfectly nested incidence matrix. We will proceed adding rows to the dataframe df_theo. A caveat is represented by the fact that, after having removed links at random, some species remain detached from the network. One needs to remove the corresponding nodes (theoretical species) from the network because they actually are not part of it. As a result, the diluted nested incidence matrix shall have a lower dimension that the perfectly nested incidence matrix. This has to be considered to normalize properly the secondary extinction curves.

20% of maiximal links

We define the perfectly nested incidence matrix as input.

nested_mat <- perfect_nested(nrow(my_inc_mat), ncol(my_inc_mat))

Then we dilute it till we are nominally left with 20% of the maximum possible number of links:

# leave roughly 0.2 of the possible links  
perc_links <- 0.2
diluted_mat <- diluted_matrix(nested_mat, perc_links)
dim(diluted_mat) 
# create dataframe from matrix 
diluted_df <- species_df_from_matrix(diluted_mat)
dim(diluted_df)
# cleanup unconnected nodes
cols <- colnames(diluted_df)
diluted_df <- diluted_df[which(rowSums(diluted_df[cols])!=0),]

#  check dimensions to be used in the plot 
dim(diluted_df)

Note that dim(diluted_df) tells us which number we need to put in the ggplot command in order to normalize the secondary extinction curves properly.
We now compute the curves for this level of dilution of links and append rows to the dataframe df_theo:

# name of the netowrk inn. the dataframe 
my_nw_name <- "diluted 0.2" 
strategy_vec <- c("RND","MTL","LTM")
conn <- as.double(sum(diluted_df))/(ncol(diluted_df)*nrow(diluted_df))

# ACHTUNG use same trick as before: do not initialize the dataframe to zero but just append new results 

for(removal_strategy in strategy_vec){
  iterations <- 10  
  if(removal_strategy=="MTL") iterations <- 30
  df_theo <- rbind(df_theo, remove_rows(diluted_df, iterations, removal_strategy, 645) %>%
                     mutate("network_name" = my_nw_name, 
                            "strategy" = removal_strategy, 
                            "connectance" = conn))
}

As usual, we recommend to give a look at the dataframe:

formattable(df_theo)

Should you wish to repeat your simulation, you can remove the dataset you have just computed from the dataframe df_theo running the following command

df_theo <- filter(df_theo, network_name!="diluted 0.2")

Task

Plot the secondary extinction curves of this diluted network against the perfectly nested one. Remember to replace nrow(my_inc_mat) and ncol(my_inc_mat) with the proper number so that both the horizontal and vertical axis have data in the interval between 0 and 1.

ggplot() +
  ggtitle(paste0("perfectly nested vs diltued 0.2")) +
  geom_line(data = filter(df_theo, strategy=="RND",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
            color = "black") +
  geom_line(data = filter(df_theo, strategy=="LTM",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green") +
  geom_line(data = filter(df_theo, strategy=="MTL",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "red",linetype = "dotted") +
  geom_point(data = filter(df_theo, strategy=="RND", network_name=="diluted 0.2"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="LTM", network_name=="diluted 0.2"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="MTL", network_name=="diluted 0.2"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "red",shape = 2) +
  ylab(TeX("$f_{plants}$")) +
  xlab(TeX("$f_{animals}$"))

10% of maiximal links

Repeat the same calculation as above with a nominal number of left links equal to 10% of the maximum possible number of links (run the underlying scripts).

# leave roughly 0.1 of the possible links  
perc_links <- 0.1
diluted_mat <- diluted_matrix(nested_mat, perc_links)
dim(diluted_mat) 
# create dataframe from matrix 
diluted_df <- species_df_from_matrix(diluted_mat)
dim(diluted_df)
# cleanup unconnected nodes
cols <- colnames(diluted_df)
diluted_df <- diluted_df[which(rowSums(diluted_df[cols])!=0),]

#  check dimensions to be used in the plot 
dim(diluted_df)

Compute the secondary extinction curve and append new rows to the dataframe df_theo:

my_nw_name <- "diluted 0.1" 
strategy_vec <- c("RND","MTL","LTM")
conn <- as.double(sum(diluted_df))/(ncol(diluted_df)*nrow(diluted_df))

# ACHTUNG use same trick as before: do not initialize the dataframe to zero but just append new results 

for(removal_strategy in strategy_vec){
  iterations <- 10  
  if(removal_strategy=="MTL") iterations <- 30
  df_theo <- rbind(df_theo, remove_rows(diluted_df, iterations, removal_strategy, 645) %>%
                     mutate("network_name" = my_nw_name, 
                            "strategy" = removal_strategy, 
                            "connectance" = conn))
}

Plot the results and compare them against those obtained for a perfectly nested incidence matrix:

ggplot() +
  ggtitle(paste0("perfectly nested vs diltued 0.1")) +
  geom_line(data = filter(df_theo, strategy=="RND",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
            color = "black") +
  geom_line(data = filter(df_theo, strategy=="LTM",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green") +
  geom_line(data = filter(df_theo, strategy=="MTL",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "red") +
  geom_point(data = filter(df_theo, strategy=="RND", network_name=="diluted 0.1"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="LTM", network_name=="diluted 0.1"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="MTL", network_name=="diluted 0.1"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "red",shape = 2) +
  ylab(TeX("$f_{plants}$")) +
  xlab(TeX("$f_{animals}$"))

5% of maiximal links

Repeat the same calculation as above with a nominal number of left links equal to 5% of the maximum possible number of links (run the underlying scripts).

# leave roughly 0.05 of the possible links  
perc_links <- 0.05
diluted_mat <- diluted_matrix(nested_mat, perc_links)
dim(diluted_mat) 
# create dataframe from matrix 
diluted_df <- species_df_from_matrix(diluted_mat)
dim(diluted_df)
# cleanup unconnected nodes
cols <- colnames(diluted_df)
diluted_df <- diluted_df[which(rowSums(diluted_df[cols])!=0),]

#  check dimensions to be used in the plot 
dim(diluted_df)

Compute the secondary extinction curve and append new rows to the dataframe df_theo:

my_nw_name <- "diluted 0.05" 
strategy_vec <- c("RND","MTL","LTM")
conn <- as.double(sum(diluted_df))/(ncol(diluted_df)*nrow(diluted_df))

# ACHTUNG use same trick as before: do not initialize the dataframe to zero but just append new results 

for(removal_strategy in strategy_vec){
  iterations <- 10  
  if(removal_strategy=="MTL") iterations <- 30
  df_theo <- rbind(df_theo, remove_rows(diluted_df, iterations, removal_strategy, 645) %>%
                     mutate("network_name" = my_nw_name, 
                            "strategy" = removal_strategy, 
                            "connectance" = conn))
}

Plot the results and compare them against those obtained for a perfectly nested incidence matrix:

ggplot() +
  ggtitle(paste0("perfectly nested vs diltued 0.05")) +
  geom_line(data = filter(df_theo, strategy=="RND",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
            color = "black",linetype = "dashed") +
  geom_line(data = filter(df_theo, strategy=="LTM",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green") +
  geom_line(data = filter(df_theo, strategy=="MTL",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "red",linetype = "dotted") +
  geom_point(data = filter(df_theo, strategy=="RND", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="LTM", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_theo, strategy=="MTL", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "red",shape = 2) +
  ylab(TeX("$f_{plants}$")) +
  xlab(TeX("$f_{animals}$"))

Questions

For diluted networks the actual connectance – reported in the column connectance of the dataframe df_theo – is systematically larger than the nominal fraction left links (0.2, 0.1, 0.05). Explain with your words why.
What is the effect of increasing the degree of dilution of the perfectly nested matrix?

7.4.1 Diltued simulated networks vs experimental networks

Compute the connectance of the experimental network you have chosen using the following command

conn_exp <- as.double(sum(my_inc_mat))/(ncol(my_inc_mat)*nrow(my_inc_mat))

and select among the simulated secondary extinction curves the one whose true connectance is closer to the one of the experimental pollination network.

Plot both datasets and comment your observation.

ggplot() +
  ggtitle(paste0("experiments vs diltued xxx vs perfectly nested")) +
  geom_point(data = filter(df_exp, strategy=="RND", network_name=="M_PL_054"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
             color = "black",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="LTM", network_name=="M_PL_054"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "dark green",shape = 2) +
  geom_point(data = filter(df_exp, strategy=="MTL", network_name=="M_PL_054"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
             color = "red",shape = 2) +
  geom_line(data = filter(df_theo, strategy=="RND",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
            color = "black") +
  geom_line(data = filter(df_theo, strategy=="LTM",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green") +
  geom_line(data = filter(df_theo, strategy=="MTL",network_name=="perfectly nested"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "red") +
  geom_line(data = filter(df_theo, strategy=="RND", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))), 
            color = "black",linetype = "dotted") +
  geom_line(data = filter(df_theo, strategy=="LTM", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "dark green",linetype = "dotted") +
  geom_line(data = filter(df_theo, strategy=="MTL", network_name=="diluted 0.05"), aes(removed_rows/nrow(my_inc_mat), (1- removed_columns/ncol(my_inc_mat))),
            color = "red",linetype = "dotted") +
  ylab(TeX("$f_{plants}$")) +
  xlab(TeX("$f_{animals}$"))